Question

【题目】如图，四边形为正方形，分别为的中点，以为折痕把折起，使点到达点的位置，且.

（1）证明：平面平面；

（2）求与平面所成角的正弦值.

Answer 1

【答案】(1)证明见解析.

(2) .

【解析】分析：(1)首先从题的条件中确定相应的垂直关系，即BF⊥PF，BF⊥EF，又因为，利用线面垂直的判定定理可以得出BF⊥平面PEF，又平面ABFD，利用面面垂直的判定定理证得平面PEF⊥平面ABFD.

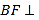(2)结合题意，建立相应的空间直角坐标系，正确写出相应的点的坐标，求得平面ABFD的法向量，设DP与平面ABFD所成角为，利用线面角的定义，可以求得，得到结果.

详解：（1）由已知可得，BF⊥PF，BF⊥EF，又，所以BF⊥平面PEF.

又平面ABFD，所以平面PEF⊥平面ABFD.

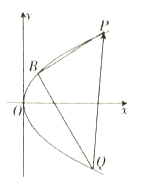
（2）作PH⊥EF，垂足为H.由（1）得，PH⊥平面ABFD.

以H为坐标原点，的方向为y轴正方向，为单位长，建立如图所示的空间直角坐标系Hxyz.

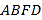
由（1）可得，DE⊥PE.又DP=2，DE=1，所以PE=.又PF=1，EF=2，故PE⊥PF.

可得.

则 为平面ABFD的法向量.

设DP与平面ABFD所成角为，则.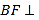

所以DP与平面ABFD所成角的正弦值为.