题目内容
已知椭圆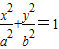
的左、右焦点分别为F1、F2，且|F1F2|=2c，点A在椭圆上，
，
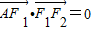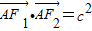，则椭圆的离心率e=（ ）A．
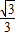
B．
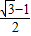
C．
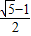
D．
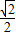
【答案】分析：本题考查的知识点是平面向量的数量积运算及椭圆的简单性质，由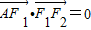
，
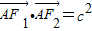，我们将两式相减后得到AF1的长度，再根据椭圆的定义，即可找到a与c之间的数量关系，进而求出离心率e．
解答：解：∵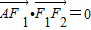
∴AF1⊥F1F2
即A点的横坐标与左焦点相同
又∵A在椭圆上，
∴A（-C，±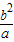
）
又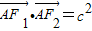
∴
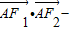
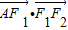=c2
即
=
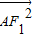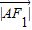2=c2
即AF1=c
则2a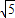=c+
c
∴e=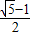
故选C
点评：求椭圆的离心率，即是在找a与c之间的关系，我们只要根据已知中的其它条件，构造方程（组），或者进行转化，转化为一个关于e的方程，解方程（组），易得e值．
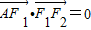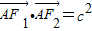，，我们将两式相减后得到AF1的长度，再根据椭圆的定义，即可找到a与c之间的数量关系，进而求出离心率e．解答：解：∵
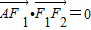
∴AF1⊥F1F2
即A点的横坐标与左焦点相同
又∵A在椭圆上，
∴A（-C，±
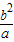）又
∴
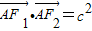
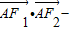
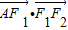=c2即
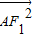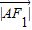=2=c2即AF1=c
则2a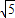=c+
c∴e=
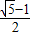
故选C
点评：求椭圆的离心率，即是在找a与c之间的关系，我们只要根据已知中的其它条件，构造方程（组），或者进行转化，转化为一个关于e的方程，解方程（组），易得e值．
练习册系列答案
阅读快车系列答案
相关题目
的左、右焦点分别为
，其右准线上
上存在点
（点
轴上方），使
为等腰三角形．
的范围；
到两焦点
，求
的左、右焦点分别为
，
，
点
是椭圆的一个顶点，△
是等腰直角三角形．
分别作直线
，
交椭圆于
，
两点，设两直线的斜率分别为
，
，且
，证明：直线
过定点（
）．
的左、右焦点分别为F1、F2，其中
的焦点，M是C1与C2在第一象限的交点，且
上，求直线AC的方程。
的左、右焦点分别为
、
，离心率
，右准线方程为
．
与该椭圆交于M、N两点，且
，求直线