题目内容
（2011•重庆模拟）已知函数f（x）=|x|-3，关于x的方程f2（x）-4|f（x）|+k=0恰有8个不同的实根，则实数k的取值范围是
（3，4）
（3，4）
．分析：关于x的方程f2（x）-4|f（x）|+k=0恰有8个不同的实根，即函数g（x）=-f2（x）+4|f（x）|图象与直线y=k有8个交点，画出图象可得．
解答：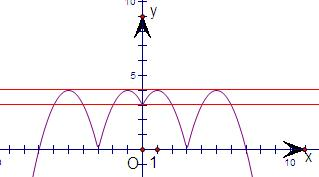
解：关于x的方程f2（x）-4|f（x）|+k=0
?（|x|-3）2-4||x|-3|+k=0
?-（|x|-3）2+4||x|-3|=k，
函数g（x）=-f2（x）+|f（x）|图象，如图所示，
由图象知，当g（x）=-f2（x）+4|f（x）|图象与直线y=k有8个交点时，
实数k的取值范围为（3，4），
故答案为（3，4）．
解：关于x的方程f2（x）-4|f（x）|+k=0?（|x|-3）2-4||x|-3|+k=0
?-（|x|-3）2+4||x|-3|=k，
函数g（x）=-f2（x）+|f（x）|图象，如图所示，
由图象知，当g（x）=-f2（x）+4|f（x）|图象与直线y=k有8个交点时，
实数k的取值范围为（3，4），
故答案为（3，4）．
点评：此题是个中档题．本题考查了分段函数，以及函数与方程的思想，数形结合的思想．
练习册系列答案
相关题目
（2011•重庆模拟）已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，-π＜φ＜π）的部分图象如图所示，则函数f（x）的解析式为（ ）