题目内容
若函数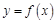 同时满足:(ⅰ)对于定义域内的任意
同时满足:(ⅰ)对于定义域内的任意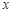 ,恒有
,恒有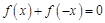 ;(ⅱ)对于定义域内的任意
;(ⅱ)对于定义域内的任意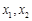 ,当
,当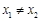 时,恒有
时,恒有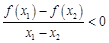 ,则称函数
,则称函数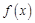 为“二维函数”.现给出下列四个函数:
为“二维函数”.现给出下列四个函数:
①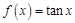 ;②
;②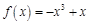 ;③
;③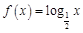 ;④
;④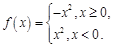
其中能被称为“二维函数”的有_____________(写出所有满足条件的函数的序号).
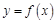 同时满足:(ⅰ)对于定义域内的任意
同时满足:(ⅰ)对于定义域内的任意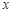 ,恒有
,恒有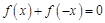 ;(ⅱ)对于定义域内的任意
;(ⅱ)对于定义域内的任意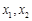 ,当
,当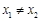 时,恒有
时,恒有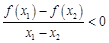 ,则称函数
,则称函数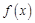 为“二维函数”.现给出下列四个函数:
为“二维函数”.现给出下列四个函数:①
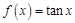 ;②
;②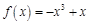 ;③
;③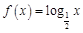 ;④
;④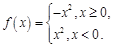
其中能被称为“二维函数”的有_____________(写出所有满足条件的函数的序号).
④
试题分析:首先明确二维函数的定义,要满足函数是奇函数,同时定义域内递减函数,因此分析函数①
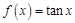 ,正切函数满足奇函数,但是在定义域内不是递减的,故不是二维函数;
,正切函数满足奇函数,但是在定义域内不是递减的,故不是二维函数;②
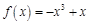 ,由于f(-x)=
,由于f(-x)=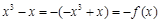 因此是奇函数,同时利用单调性的性质可知,函数不是递减函数,不满足题意;
因此是奇函数,同时利用单调性的性质可知,函数不是递减函数,不满足题意;③
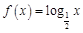 中是非奇非偶函数,不符合题意;
中是非奇非偶函数,不符合题意;④
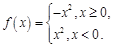 ,
,当
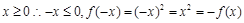
当
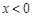 ,
,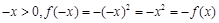
故可知是奇函数,同时在定义域内每一段都是减函数,同时在x=0时,函数值为零,符合函数递减性,故④
点评:解决该试题的关键是对于分段函数的分析和应用。注意到分段函数的奇偶性的判定,以及整个函数在定义域内递减时,注意断点的函数值的大小关系。属于中档题。

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
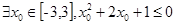 ,则对命题p的否定是( )
,则对命题p的否定是( )

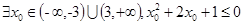
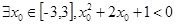
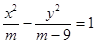 表示焦点在y轴上的椭圆;命题q:双曲线
表示焦点在y轴上的椭圆;命题q:双曲线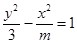 的离心率
的离心率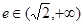 ,若p、q有且只有一个为真,求m的取值范围。
,若p、q有且只有一个为真,求m的取值范围。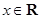 ,都有
,都有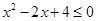 ”的否定为( )
”的否定为( )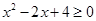
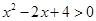
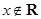 ,使
,使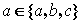 ,q:
,q: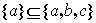
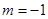 ”是“直线
”是“直线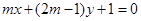 和线
和线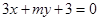 垂直”的
垂直”的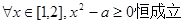 ,命题q:
,命题q: ,
,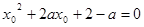 若“p且q”为真命题,求实数a的取值范围。
若“p且q”为真命题,求实数a的取值范围。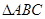 中,若
中,若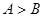 ,则
,则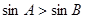 ;
;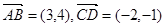 ,则
,则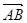 在
在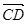 上的投影为
上的投影为 ;
;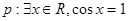 ,
,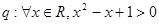 ,则“
,则“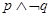 ”为假命题;
”为假命题;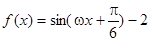
 的导函数的最大值为
的导函数的最大值为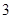 ,则函数
,则函数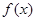 的图
的图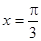 对称.
对称.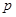 :
: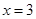 ,
, 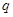 :
: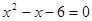 ,那么
,那么