题目内容
在抛物线y2=2x上求一点P,使点P到直线x-y+3=0的距离最短并求出距离的最小值.
思路解析:本例解法较多.思路一:设抛物线上一点的坐标,直接利用点到直线的距离公式求出距离,再求距离的最小值,同时有一定的运算量;思路二:先求出与已知直线平行的抛物线的切线l′,再求出切点坐标即可. 解法一:设点P(x0,y0)是y2=2x上任意一点,则点P到直线x-y+3=0的距离为d= 解法二:设与直线x-y+3=0平行的切线为x-y+t=0,与y2=2x联立消去x得y2-2y+2t=0,由Δ=0可得t=
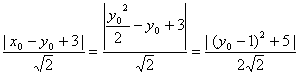 ,当y0=1时,dmin=
,当y0=1时,dmin=![]() =
=![]() .此时,点P的坐标为(
.此时,点P的坐标为(![]() ,1).
,1).![]() ,此时y=1,x=
,此时y=1,x=![]() .∴点P的坐标为(
.∴点P的坐标为(![]() ,1).两平行线间的距离就是所求的点P到直线的最小距离为dmin=
,1).两平行线间的距离就是所求的点P到直线的最小距离为dmin=![]() =
=![]() .
. 练习册系列答案
练习册系列答案
期末冲刺智胜卷系列答案
期末冲刺必备模拟试卷系列答案
培优新航标系列答案
培优大视野系列答案
仁爱地理同步练习册系列答案
牛津英语活动练习手册系列答案
牛津英语基础训练系列答案
牛津英语随堂讲与练系列答案
牛津英语一课一练系列答案
中考真题及模拟试题汇编系列答案
相关题目
(文)圆心在抛物线y2=2x上,且与该抛物线的准线和x轴都相切的圆的方程是( )
A、(x-
| ||||||
B、(x-
| ||||||
C、(x-
| ||||||
D、(x-
|