题目内容
已知定义在区间(0,+∞)上的函数f(x)满足f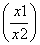 =f(x1)-f(x2),且当x>1时,f(x)<0.
=f(x1)-f(x2),且当x>1时,f(x)<0.
(1)求f(1)的值;
(2)判断f(x)的单调性;
(3)若f(3)=-1,求f(x)在[2,9]上的最小值.
解:(1)令x1=x2>0,代入得f(1)=f(x1)-f(x1)=0,故f(1)=0.
(2)任取x1,x2∈(0,+∞),且x1>x2,
则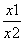 >1,由于当x>1时,f(x)<0,
>1,由于当x>1时,f(x)<0,
所以f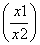 <0,即f(x1)-f(x2)<0,
<0,即f(x1)-f(x2)<0,
因此f(x1)<f(x2),
所以函数f(x)在区间(0,+∞)上是单调递减函数.
(3)∵f(x)在(0,+∞)上是单调递减函数.
∴f(x)在[2,9]上的最小值为f(9).
由f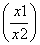 =f(x1)-f(x2)得,
=f(x1)-f(x2)得,
f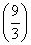 =f(9)-f(3),
=f(9)-f(3),
而f(3)=-1,∴f(9)=-2.
∴f(x)在[2,9]上的最小值为-2.

练习册系列答案
相关题目
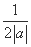 +
+  的最小值为
的最小值为 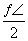 +2kπ(k∈Z)”是“函数y=sin(2x+φ)为偶函数”的充要条件
+2kπ(k∈Z)”是“函数y=sin(2x+φ)为偶函数”的充要条件
 在
在 上是减函数,则
上是减函数,则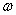 的取值范围是( )
的取值范围是( ) A
A 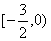 B
B 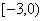 C
C 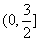 D
D 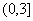
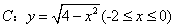 与函数
与函数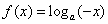 及函数
及函数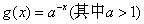 的图像分别交于
的图像分别交于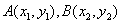 ,则
,则 的值为
的值为 为奇函数,则a=( )
为奇函数,则a=( )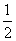 B.
B.
 D.1
D.1