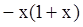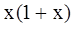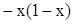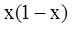题目内容
已知函数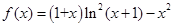 ,
,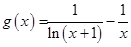 .
.
(Ⅰ)判定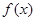 在
在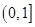 上的单调性;
上的单调性;
(Ⅱ)求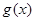 在
在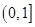 上的最小值;
上的最小值;
(Ⅲ)若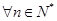 ,
, 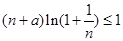 ,求实数
,求实数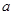 的取值范围.
的取值范围.
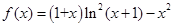 ,
,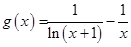 .
.(Ⅰ)判定
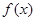 在
在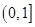 上的单调性;
上的单调性;(Ⅱ)求
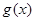 在
在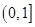 上的最小值;
上的最小值;(Ⅲ)若
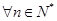 ,
, 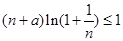 ,求实数
,求实数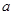 的取值范围.
的取值范围. 解:(Ⅰ∴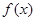 在
在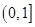 上的单调递减.
上的单调递减.
(Ⅱ)∴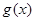 在
在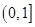 上的最小值为
上的最小值为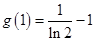
(Ⅲ)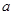 的取值范围是
的取值范围是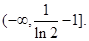
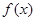 在
在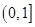 上的单调递减.
上的单调递减. (Ⅱ)∴
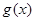 在
在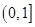 上的最小值为
上的最小值为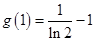
(Ⅲ)
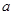 的取值范围是
的取值范围是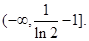
本试题主要是考查了导数在研究函数的运用
(1)根据已知条件,求解定义域和导数,然后根据导数的符号与函数单调性的关系求解得到单调区间。
(2)同上,求解导数,分析单调性,然后得到极值,从而求解最值。
(3)要证明不等式恒成立,分离参数的思想,构造新函数,求解导数得到最值,进而得到参数a的范围。
(1)根据已知条件,求解定义域和导数,然后根据导数的符号与函数单调性的关系求解得到单调区间。
(2)同上,求解导数,分析单调性,然后得到极值,从而求解最值。
(3)要证明不等式恒成立,分离参数的思想,构造新函数,求解导数得到最值,进而得到参数a的范围。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
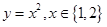 的“同族函数”有( )
的“同族函数”有( )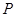 (元)与时间
(元)与时间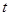 (天)的函数关系是:
(天)的函数关系是: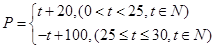 ,该商品的日销量
,该商品的日销量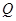 (件)与时间
(件)与时间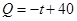
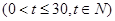 ,求该商品的日销量金额的最大值,并指出日销售金额最多的一天是30天中的第几天。
,求该商品的日销量金额的最大值,并指出日销售金额最多的一天是30天中的第几天。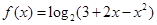 .
. 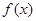 的定义域;
的定义域;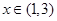 上是减函数;
上是减函数;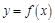 是
是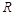 上的偶函数,且
上的偶函数,且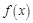 在
在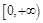 上是减函数,若
上是减函数,若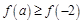 ,则
,则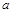 的取值范围是( )
的取值范围是( )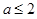
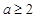
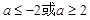
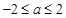
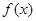 为定义在
为定义在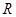 上的奇函数,当
上的奇函数,当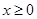 时,
时,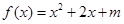 (
(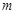 为常数),则
为常数),则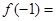 ;
;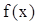 为奇函数,若
为奇函数,若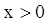 时,
时,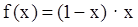 ,则
,则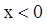 时,
时,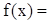 ( )
( )