题目内容
在等差数列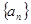 中,
中,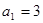 ,其前
,其前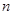 项和为
项和为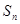 ,等比数列
,等比数列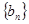 的各项均为正数,
的各项均为正数,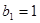 ,公比为
,公比为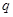 ,且
,且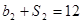 ,
, 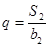 .
.
(Ⅰ)求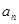 与
与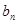 ;
;
(Ⅱ)证明: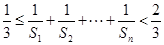 .
.
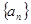 中,
中,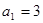 ,其前
,其前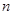 项和为
项和为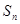 ,等比数列
,等比数列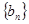 的各项均为正数,
的各项均为正数,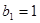 ,公比为
,公比为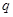 ,且
,且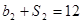 ,
, 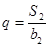 .
.(Ⅰ)求
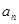 与
与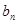 ;
;(Ⅱ)证明:
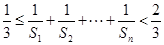 .
.(Ⅰ) ,
, .
.
(Ⅱ)由 ,
,
得 .
.
求得

因为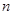 ≥
≥ ,所以
,所以 ≤
≤ ,于是
,于是 ≤
≤ ,
,
得出 ≤
≤ 。
。
 ,
, .
.(Ⅱ)由
 ,
,得
 .
.求得


因为
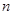 ≥
≥ ,所以
,所以 ≤
≤ ,于是
,于是 ≤
≤ ,
,得出
 ≤
≤ 。
。试题分析:(Ⅰ)设
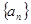 的公差为
的公差为 ,
,因为
 所以
所以 3分
3分解得
 或
或 (舍),
(舍), .
.故
 ,
, . 6分
. 6分(Ⅱ)因为
 ,
,所以
 . 9分
. 9分故


 11分
11分因为
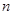 ≥
≥ ,所以
,所以 ≤
≤ ,于是
,于是 ≤
≤ ,
,所以
 ≤
≤ .
.即
 ≤
≤ 13分
13分点评:中档题,本题具有较强的综合性,本解答从确定通项公式入手,从而求得了
 ,进一步转化成数列
,进一步转化成数列 求和问题,利用“裂项相消法”化简,达到证明不等式的目的。
求和问题,利用“裂项相消法”化简,达到证明不等式的目的。
练习册系列答案
相关题目
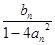 (n∈N*)且点P1的坐标为(1,-1).(1)求过点P1,P2的直线l的方程;
(n∈N*)且点P1的坐标为(1,-1).(1)求过点P1,P2的直线l的方程;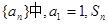 是数列
是数列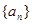 的前n项和,对任意
的前n项和,对任意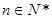 ,有2Sn=2
,有2Sn=2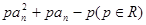 .
.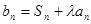 ,(
,(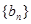 从第二项起每一项都比它的前一项大,求
从第二项起每一项都比它的前一项大,求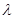 的取值范围.
的取值范围.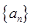 的各项排成如图所示的三角形数阵,数阵中每一行的第一个数
的各项排成如图所示的三角形数阵,数阵中每一行的第一个数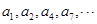 构成等差数列
构成等差数列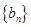 ,
,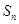 是
是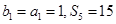
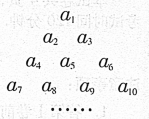
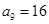 ,求
,求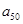 的值;
的值;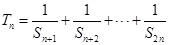 ,求
,求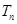 .
.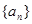 的前n项和为
的前n项和为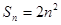
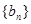 为等比数列,且
为等比数列,且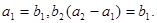
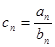 ,求数列
,求数列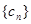 的前n项和
的前n项和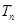 。
。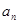 }中,al=1,a2=2,2
}中,al=1,a2=2,2 2+
2+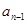 2 (n≥2),则a6等于
2 (n≥2),则a6等于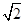
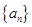 中,
中,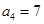 ,且
,且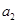 、
、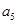 、
、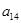 成等比数列.
成等比数列.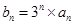 ,求数列
,求数列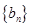 的前
的前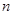 项的和
项的和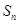 .
.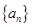 的前
的前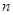 项和为
项和为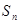 .已知
.已知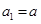 ,
,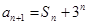 ,
, .
.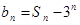 ,求数列
,求数列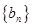 的通项公式;
的通项公式;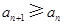 ,
,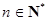 ,求
,求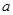 的取值范围.
的取值范围.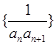 的前100项和为( )
的前100项和为( )


