题目内容

三棱柱ABC-A₁B₁C₁底面是等边三角形，顶点A₁在底面的射影为点B，且△ABA₁是一个等腰直角三角形，则异面直线AB与B₁C所成的角大小为

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

B
分析：建立坐标系，写出各点的坐标，求出 $\text{[math]}$ 的坐标，利用向量的数量积公式求出 $\text{[math]}$ 的夹角余弦，取其绝对值即为异面直线AB与B₁C所成的角的余弦．
解答：取AC的中点D，以BD为x轴，以BA₁为z轴，过B平行于AC的直线为y轴建立坐标系，设底面的边长为1，则侧棱长为 $\text{[math]}$ 则
A（ $\text{[math]}$ ），B（0，0，0），C（ $\text{[math]}$ ）， $\text{[math]}$
$\text{[math]}$ ， $\text{[math]}$
∴ $\text{[math]}$
∵ $\text{[math]}$
∴ $\text{[math]}$ = $\text{[math]}$
设异面直线AB与B₁C所成的角为θ
∴ $\text{[math]}$
∴ $\text{[math]}$
故选B
点评：解决立体几何中的点、线、面的位置关系及度量关系常借助的工具是空间向量．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

相关题目

在三棱柱ABC-A₁B₁C₁中，侧面AA₁B₁B是边长为2的正方形，点C在平面AA₁B₁B上的射影H恰好为A₁B的中点，且CH=

，设D为CC₁中点，
（Ⅰ）求证：CC₁⊥平面A₁B₁D；
（Ⅱ）求DH与平面AA₁C₁C所成角的正弦值．

如图（1）是一个水平放置的正三棱柱ABC-A₁B₁C₁，D是棱BC的中点．正三棱柱的主视图如图（2）．
（Ⅰ）图（1）中垂直于平面BCC₁B₁的平面有哪几个？（直接写出符合要求的平面即可，不必说明或证明）
（Ⅱ）求正三棱柱ABC-A₁B₁C₁的体积；
（Ⅲ）证明：A₁B∥平面ADC₁．

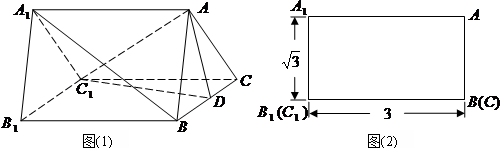
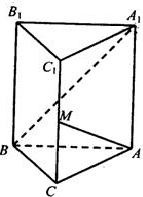如图，在直三棱柱ABC-A₁B₁C₁中，∠ACB=90°，∠BAC=30°，BC=1，AA1=

，M是棱CC₁的中点，
（1）求证：A₁B⊥AM；
（2）求直线AM与平面AA₁B₁B所成角的正弦值．

如图：在直三棱柱ABC-A₁B₁C₁中，已知AB=A₁A，AC=BC，点D、E分别为C₁C、AB的中点，O为A₁B与AB₁的交点．
（Ⅰ）求证：EC∥平面A₁BD；
（Ⅱ）求证：AB₁⊥平面A₁BD．

如图所示，在正三棱柱ABC—A₁B₁C₁中，BB₁=BC=2，且M是BC的中点，点N在CC₁上。

（1）试确定点N的位置，使AB₁⊥MN；

（2）当AB₁⊥MN时，求二面角M—AB₁—N的大小。