题目内容
已知正方形ABCD一边CD所在直线的方程为x+3y-13=0,对角线AC,BD的交点为P(1,5)
求(1)正方形ABCD其它三边所在直线的方程:
(2)正方形ABCD的外接圆方程.
求(1)正方形ABCD其它三边所在直线的方程:
(2)正方形ABCD的外接圆方程.
分析:(1)先计算P(1,5)到lCD的距离d=
,设lAB:x+3y+m=0,设P(1,5)到lAB的距离也等于d,由此入手能够求出正方形ABCD其它三边所在直线的方程.
(2)正方形ABCD的外接圆的半径r=
d=
,圆心P(1,5),由此能求出正方形ABCD的外接圆的方程.
| 3 | ||
|
(2)正方形ABCD的外接圆的半径r=
| 2 |
| 3 | ||
|
解答:解:(1)P(1,5)到lCD的距离d,则d=
,
∵lAB∥lCD,
设lAB:x+3y+m=0
设P(1,5)到lAB的距离也等于d,
则
=
,
又m≠-13,
∴m=-19,lAB:x+3y-19=0,lCD:x+3y-13=0,
∵lAD⊥lCD设lAD:3x-y+n=0,
则P(1,5)到lAD的距离等于P(1,5)到lBC的距离,
且都等于d=
,
=
,
n=5,n=-1,lAD:3x-y+5=0,lBC:3x-y-1=0
所以,正方形 ABCD其它三边所在直线的方程x+3y-19=0,3x-y+5=0,3x-y-1=0
(2)正方形ABCD的外接圆的半径r=
d=
,
圆心P(1,5)
所以,正方形ABCD的外接圆的方程(x-1)2+(y-5)2=
| 3 | ||
|
∵lAB∥lCD,
设lAB:x+3y+m=0
设P(1,5)到lAB的距离也等于d,
则
| |m+16| | ||
|
| 3 | ||
|
又m≠-13,
∴m=-19,lAB:x+3y-19=0,lCD:x+3y-13=0,
∵lAD⊥lCD设lAD:3x-y+n=0,
则P(1,5)到lAD的距离等于P(1,5)到lBC的距离,
且都等于d=
| 3 | ||
|
| |n-2| | ||
|
| 3 | ||
|
n=5,n=-1,lAD:3x-y+5=0,lBC:3x-y-1=0
所以,正方形 ABCD其它三边所在直线的方程x+3y-19=0,3x-y+5=0,3x-y-1=0
(2)正方形ABCD的外接圆的半径r=
| 2 |
| 3 | ||
|
圆心P(1,5)
所以,正方形ABCD的外接圆的方程(x-1)2+(y-5)2=
| 9 |
| 5 |
点评:本题考查直线方程的求法和圆的方程的求法,综合性较强,具有一定的难度.解题时要认真审题,仔细解答.

练习册系列答案
相关题目
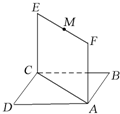 (2010•烟台一模)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
(2010•烟台一模)如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,