Question

已知关于x的方程x²+（2+i）x+4ab+（2a－b）i=0（a、bR）有实数根,

（1）求a、b应满足的条件;

（2）求实数根的取值范围.

Answer 1

解:（1）设x₀是方程的实数根,则

x₀²+（2+i）x₀+4ab+（2a－b）i=0（a、bR）,

即x₀²+2x₀+4ab+（x₀+2a－b）i=0.

 由②得x₀=b－2a,代入③,得

（b－2a）²+2（b－2a）+4ab=0.

整理得4a²+b²－4a+2b=0.                                                                                         ③

（2）方法一:由②得b=x₀+2a,代入①,得

4a²+（x₀+2a）²－4a+2（x₀+2a）=0,

即8a²+4x₀a+x₀²+2x₀=0.

∵aR,∴Δ=16x₀²－32（x₀²+2x₀）≥0,

即x₀²+4x₀≤0.∴－4≤x₀≤0.

∴方程的实数根的取值范围是［－4,0］.

方法二:将③变形为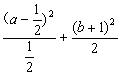=1.

令则x₀=b－2a=－2+（sinθ－cosθ）=－2+2sin（θ－

∴x₀［－4,0］.