题目内容
已知直线l1:ax-by+4=0和直线l2:(a-1)x+y+2=0,求分别满足下列条件的a,b的值
(1)直线l1过点(-3,-1),并且直线l1和l2垂直
(2)直线l1和l2平行,且直线 l1在y轴上的截距为-3.
(1)直线l1过点(-3,-1),并且直线l1和l2垂直
(2)直线l1和l2平行,且直线 l1在y轴上的截距为-3.
考点:直线的一般式方程与直线的垂直关系,直线的一般式方程与直线的平行关系
专题:直线与圆
分析:(1)当a=1,b=0时,直线l1:x+4=0,直线l2:y+2=0,此时两条直线垂直,但是直线l1不经过点(-3,-1),舍去;当b≠0时,由直线l1和l2垂直,利用斜率与垂直的关系可得:
×(1-a)=-1,又-3a+b+4=0,联立解得即可;
(2)由l1∥l2,可得
=1-a,
≠-2,又直线 l1在y轴上的截距为-3,可得
=-3.联立解得即可.
| a |
| b |
(2)由l1∥l2,可得
| a |
| b |
| 4 |
| b |
| 4 |
| b |
解答:
解:(1)当a=1,b=0时,直线l1:x+4=0,直线l2:y+2=0,此时两条直线垂直,但是直线l1不经过点(-3,-1),舍去;
当b≠0时,∵直线l1和l2垂直,∴
×(1-a)=-1,化为a(a-1)=b,又-3a+b+4=0,联立解得a=2,b=2.
∴a=2,b=2.
(2)∵l1∥l2,∴
=1-a,
≠-2,
又直线 l1在y轴上的截距为-3,∴
=-3.
联立
,解得b=-
,a=4.
当b≠0时,∵直线l1和l2垂直,∴
| a |
| b |
∴a=2,b=2.
(2)∵l1∥l2,∴
| a |
| b |
| 4 |
| b |
又直线 l1在y轴上的截距为-3,∴
| 4 |
| b |
联立
|
| 4 |
| 3 |
点评:本题考查了平行垂直与斜率的关系,考查了计算能力,属于基础题.

练习册系列答案
相关题目
若x>0,y>0,则“x2+y2>1”是“x+y>1”的( )
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知两个不重合的平面α和β,给定下列条件:
①存在直线l,使得l⊥α,且l⊥β;
②存在直线l,使得l∥α,且l∥β;
③α内有不共线的三点到β的距离相等;
④存在异面直线l,m,使得l∥α,l∥β,m∥α,m∥β;
其中,可以判定α与β平行的条件的是( )
①存在直线l,使得l⊥α,且l⊥β;
②存在直线l,使得l∥α,且l∥β;
③α内有不共线的三点到β的距离相等;
④存在异面直线l,m,使得l∥α,l∥β,m∥α,m∥β;
其中,可以判定α与β平行的条件的是( )
| A、①③ | B、①④ |
| C、①③④ | D、①②③④ |
直线y=kx+k与椭圆
+
=1的位置关系是( )
| x2 |
| 3 |
| y2 |
| 2 |
| A、相交 | B、相切 | C、相离 | D、不确定 |
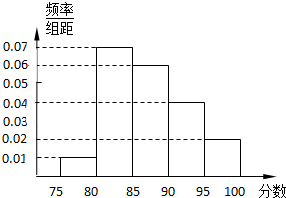 某高中进行高中生歌唱比赛,在所有参赛成绩中随机抽取100名学生的成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.现在组委会决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试.
某高中进行高中生歌唱比赛,在所有参赛成绩中随机抽取100名学生的成绩,按成绩分组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100]得到的频率分布直方图如图所示.现在组委会决定在笔试成绩高的第3,4,5组中用分层抽样抽取6名学生进入第二轮面试.