题目内容
在一个60°的二面角α-l-β的棱l上有两点A、B,线段AC?a线段BD?β并且AC⊥l,BD⊥lAC=6,BD=8,AB=4,则CD的长为
- A.2

- B.2

- C.2

- D.2
C
分析:CD的长即为向量 的模,将向量
的模,将向量  转化成
转化成 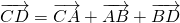 ,利用向量数量积运算求模即可.
,利用向量数量积运算求模即可.
解答: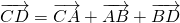 ,
, =
= ①
①
由已知, =120°∴①=36+16+64+2×6×8×cos120°=68.∴
=120°∴①=36+16+64+2×6×8×cos120°=68.∴
即CD的长为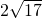
故选C.
点评:本题考查空间距离求解,二面角的定义及应用.考查转化,空间想象、计算能力.
分析:CD的长即为向量
 的模,将向量
的模,将向量  转化成
转化成 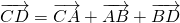 ,利用向量数量积运算求模即可.
,利用向量数量积运算求模即可.解答:
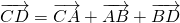 ,
, =
= ①
①由已知,
 =120°∴①=36+16+64+2×6×8×cos120°=68.∴
=120°∴①=36+16+64+2×6×8×cos120°=68.∴
即CD的长为
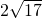
故选C.
点评:本题考查空间距离求解,二面角的定义及应用.考查转化,空间想象、计算能力.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
在一个45°的二面角的一个面内有一条直线与二面角的棱成45°,则此直线与二面角的另一个面所成的角为( )
| A、30° | B、45° | C、60° | D、90° |