题目内容
已知函数![]() (
(![]() ,实数
,实数![]() ,
,![]() 为常数).
为常数).
(Ⅰ)若![]() ,求
,求![]() 在
在![]() 处的切线方程;
处的切线方程;
(Ⅱ)若![]() ,讨论函数
,讨论函数![]() 的单调性.
的单调性.
解:(Ⅰ)因为![]() ,所以函数
,所以函数![]() ,
,![]()
又![]() ,
,![]() -------------------------------------2分
-------------------------------------2分
所以![]()
即![]() 在
在![]() 处的切线方程为
处的切线方程为![]() -----------------------------5分
-----------------------------5分
(Ⅱ)因为![]() ,所以
,所以![]() ,则
,则
![]()
![]()
令![]() ,得
,得![]() ,
,![]() .------------------------------------7分
.------------------------------------7分
(1)当![]() ,即
,即![]() 时,函数
时,函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ;--8分
;--8分
(2)当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
所以,函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() ;-------9分
;-------9分
(3)当![]() ,即
,即![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;----------10分
;----------10分
(4)当![]() ,即
,即![]() 时,
时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
所以函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() ;----------12分
;----------12分
综上,当![]() 时,函数
时,函数![]() 的单调递减区间为
的单调递减区间为![]() ,单调递增区间为
,单调递增区间为![]() ;当
;当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() ;当
;当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;当
;当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]() ,单调递减区间为
,单调递减区间为![]() .-----------------------13分
.-----------------------13分

练习册系列答案
相关题目
 (
( ,实数
,实数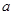 ,
,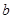 为常数).
为常数).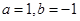 ,求
,求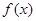 在
在 处的切线方程;
处的切线方程;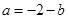 ,讨论函数
,讨论函数 (
( ,实数
,实数 ,
, 为常数).
为常数). ,求函数
,求函数 的极值;
的极值; ,讨论函数
,讨论函数