题目内容
已知g（x）=loga|x+1|（a＞0且a≠1）在（-1，0）上有g（x）＞0，则f（x）=a|x+1|是（ ）
分析：根据g（x）在（-1，0）上有g（x）＞0可判断a的范围，由a的范围结合选项即可判断答案．
解答：解：当x∈（-1，0）时，x+1∈（0，1），g（x）=loga|x+1|=loga（x+1），
因为g（x）＞0，所以0＜a＜1，
所以当x∈（-∞，-1）时，f（x）=a|x+1|=a-x-1单调递增，
故选C．
因为g（x）＞0，所以0＜a＜1，
所以当x∈（-∞，-1）时，f（x）=a|x+1|=a-x-1单调递增，
故选C．
点评：本题考查对数函数的单调性及绝对值的性质，考查学生分析问题解决问题的能力，属中档题．
练习册系列答案
全能测控期末小状元系列答案
相关题目
已知函数f(x)＝log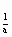
(2－x)在其定义域上单调递增，则函数g(x)＝loga(1－x2)的单调递减区间是
[ ]
|
A．(－∞，0) |
B．(－1，0) |
|
C．[0，＋∞] |
D．[0，1] |