题目内容
已知x,y,z∈R+,且x+y+z=1
(1)若2x2+3y2+6z2=1,求x,y,z的值.
(2)若2x2+3y2+tz2≥1恒成立,求正数t的取值范围.
(1)若2x2+3y2+6z2=1,求x,y,z的值.
(2)若2x2+3y2+tz2≥1恒成立,求正数t的取值范围.
(1)x=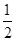 ,y=
,y=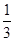 ,z=
,z=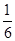 (2)t≥6
(2)t≥6
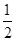 ,y=
,y=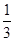 ,z=
,z=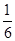 (2)t≥6
(2)t≥6(1)∵(2x2+3y2+6z2)( )≥(x+y+z)2=1,当且仅当
)≥(x+y+z)2=1,当且仅当 时取“=”.∴2x=3y=6z,
时取“=”.∴2x=3y=6z,
又∵x+y+z=1,∴x=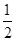 ,y=
,y=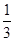 ,z=
,z=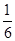 .
.
(2)∵(2x2+3y2+tz2)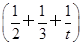 ≥(x+y+z)2=1,∴(2x2+3y2+tz2)min=
≥(x+y+z)2=1,∴(2x2+3y2+tz2)min=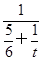 .
.
∵2x2+3y2+tz2≥1恒成立,∴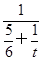 ≥1.∴t≥6.
≥1.∴t≥6.
 )≥(x+y+z)2=1,当且仅当
)≥(x+y+z)2=1,当且仅当 时取“=”.∴2x=3y=6z,
时取“=”.∴2x=3y=6z,又∵x+y+z=1,∴x=
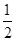 ,y=
,y=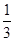 ,z=
,z=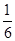 .
.(2)∵(2x2+3y2+tz2)
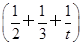 ≥(x+y+z)2=1,∴(2x2+3y2+tz2)min=
≥(x+y+z)2=1,∴(2x2+3y2+tz2)min=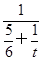 .
.∵2x2+3y2+tz2≥1恒成立,∴
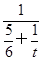 ≥1.∴t≥6.
≥1.∴t≥6.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
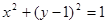 上任意一点时,不等式
上任意一点时,不等式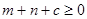 恒成立,则c的取值范围是( )
恒成立,则c的取值范围是( )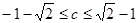
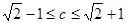
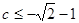
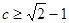
 ,B={x/ax2+bx+c
,B={x/ax2+bx+c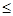 0},若
0},若 则
则 的最小值_______.
的最小值_______.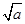 +
+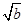 +
+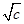 的最大值.
的最大值.