题目内容
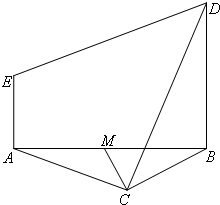
如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点.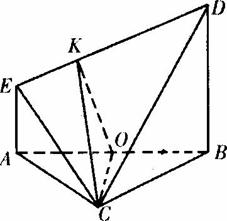
(Ⅰ)证明:CO⊥DE;
(Ⅱ)求二面角C-DE-A的大小.
答案:方法—:(Ⅰ)证明:因△ABC为等边三角形,且O为AB中点

∴CO⊥AB又∵平面ABDE⊥平面ABC ∴CO⊥平面ABDE
∵DE![]() 平面ABDE ∴CO⊥DE
平面ABDE ∴CO⊥DE
(Ⅱ)解:过O作OK⊥DE于K,连接CK,则由三垂线定理得
CK⊥ED ∴所求二面角的平面角为∠OKC
在正三角形ABC中可求得CO=![]() ,在直角梯形ABDE中可求得
,在直角梯形ABDE中可求得
KO=![]() ,tan∠OKC=
,tan∠OKC=![]() ;所以所求二面角的大小为arctan
;所以所求二面角的大小为arctan![]()
方法二:以AB的中点O为原点建立直角坐标系(如图),

则A(0,-1,0),B(0,1,0),C(![]() ,0,0),D(0,1,2),E(0,-1,1),
,0,0),D(0,1,2),E(0,-1,1),
(Ⅰ)证明:![]() =(
=(![]() ,0,0),
,0,0),![]() =(0,-2,-1),∵
=(0,-2,-1),∵![]() =0, ∴CO⊥DE,
=0, ∴CO⊥DE,
(Ⅱ)解:显然,面ABDE的一个法向量m=(1,0,0),设面DCE的一个法向量为n=(x,y,z),则
由n⊥![]() 得
得![]() x+y-z=0,由n⊥
x+y-z=0,由n⊥![]() 得2y+z=0,
得2y+z=0,
解得n=(![]() ,1,-2),|cos〈m,n〉|=
,1,-2),|cos〈m,n〉|=![]() 所以所求二面角的大小为arccos
所以所求二面角的大小为arccos![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
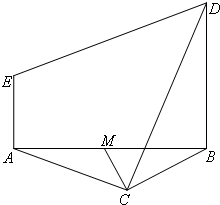 如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.
如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,BD=2AE,AE⊥AB,M为AB的中点.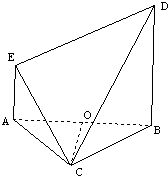 如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点.
如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点. 如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点.
如图,等边△ABC与直角梯形ABDE所在平面垂直,BD∥AE,AE⊥AB,BC=BD=2AE=2,O为AB的中点.