题目内容
如图，等边△ABC与直角梯形ABDE所在平面垂直，BD∥AE，BD=2AE，AE⊥AB，M为AB的中点．
（1）证明：CM⊥DE；
（2）在边AC上找一点N，使CD∥平面BEN．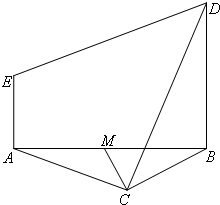
（1）证明：CM⊥DE；
（2）在边AC上找一点N，使CD∥平面BEN．
（1）证明：因为BC=AC，M为AB中点．所以CM⊥AB，
又因为平面ABC⊥平面ABDE，平面ABC∩平面ABDE=AB，CM?平面ABC，
所以CM⊥平面ABDE，
又因DE?平面ABDE，所以CM⊥DE；（7分）
（2）当
=
时，CD∥平面BEN．
连接AD交BE于点K，连接KN，
因梯形ABDE中BD∥AE，BD=2AE，
所以
=
=
，则
=
又因
=
，所以KN∥CD（14分）
又KN?平面BEN，CD?平面BEN，所以CD∥平面BEN．
又因为平面ABC⊥平面ABDE，平面ABC∩平面ABDE=AB，CM?平面ABC，
所以CM⊥平面ABDE，
又因DE?平面ABDE，所以CM⊥DE；（7分）
（2）当
| AN |
| AC |
| 1 |
| 3 |
连接AD交BE于点K，连接KN，
因梯形ABDE中BD∥AE，BD=2AE，
所以
| AK |
| KD |
| AE |
| BD |
| 1 |
| 2 |
| AK |
| AD |
| 1 |
| 3 |
又因
| AN |
| AC |
| 1 |
| 3 |
又KN?平面BEN，CD?平面BEN，所以CD∥平面BEN．
练习册系列答案
相关题目
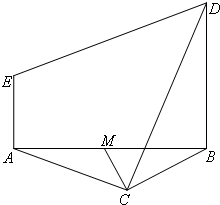如图，等边△ABC与直角梯形ABDE所在平面垂直，BD∥AE，BD=2AE，AE⊥AB，M为AB的中点．
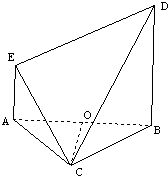如图，等边△ABC与直角梯形ABDE所在平面垂直，BD∥AE，AE⊥AB，BC=BD=2AE=2，O为AB的中点．
如图，等边△ABC与直角梯形ABDE所在平面垂直，BD∥AE，AE⊥AB，BC=BD=2AE=2，O为AB的中点．