题目内容
已知复数z1=3+4i,z2的平方根是2+3i,且函数f(x)=
.
(1)求f(
+z2);
(2)若f(z)=1+i,求z.
| 2x |
| x+1 |
(1)求f(
. |
| z1 |
(2)若f(z)=1+i,求z.
分析:(1)把复数2+3i求平方运算解得z2,求出
+z2后直接代入函数解析式,然后利用复数的除法运算化简整理;
(2)把z代入函数解析式,得到f(z)=
=1+i,整理后得到z=
,然后利用复数的除法运算化简z.
. |
| z1 |
(2)把z代入函数解析式,得到f(z)=
| 2z |
| z+1 |
| 1+i |
| 1-i |
解答:解:(1)由复数z1=3+4i,则
=3-4i,又z2的平方根是2+3i,所以z2=(2+3i)2=-5+12i.
所以
+z2=3-4i+(-5+12i)=-2+8i,
则f(
+z2)=f(-2+8i)=
=
=
=
=
+
i.
(2)由f(z)=
=1+i,
得:2z=(1+i)(z+1)=z+1+iz+i,即(1-i)z=1+i,
所以z=
=
=
=i.
. |
| z1 |
所以
. |
| z1 |
则f(
. |
| z1 |
| 2(-2+8i) |
| -2+8i+1 |
| -4+16i |
| -1+8i |
| (-4+16i)(-1-8i) |
| (-1+8i)(-1-8i) |
| 132+16i |
| 65 |
| 132 |
| 65 |
| 16 |
| 65 |
(2)由f(z)=
| 2z |
| z+1 |
得:2z=(1+i)(z+1)=z+1+iz+i,即(1-i)z=1+i,
所以z=
| 1+i |
| 1-i |
| (1+i)2 |
| (1-i)(1+i) |
| 2i |
| 2 |
点评:本题考查了复数代数形式的乘除运算,考查了复数相等的条件,复数的除法运算,采用分子分母同时乘以分母的共轭复数,是基础题.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
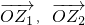 (其中O为坐标原点),记向量
(其中O为坐标原点),记向量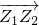 所对应的复数为z,则z的共轭复数为________.
所对应的复数为z,则z的共轭复数为________.