题目内容
已知复数z1=3-4i和z2=4-i在复平面内所对应的向量分别为
，
（其中O为坐标原点），记向量
所对应的复数为z，则z的共轭复数为
| OZ1 |
| OZ2 |
| Z1Z2 |
1-3i
1-3i
．分析：由复数
=z1=3-4i，
=z2=4-i可得z=
=
-
，从而可求得z的共轭复数
．
| OZ1 |
| OZ2 |
| Z1Z2 |
| OZ2 |
| OZ1 |
. |
| z |
解答：解：∵
=3-4i，
=4-i，
∴z=
=
-
=4-i-（3-4i）=1+3i，
∴z的共轭复数
=1-3i．
故答案为：1-3i．
| OZ1 |
| OZ2 |
∴z=
| Z1Z2 |
| OZ2 |
| OZ1 |
∴z的共轭复数
. |
| z |
故答案为：1-3i．
点评：本题考查复数的代数表示法及其几何意义，关键理解向量的运算与复数的概念，属于中档题．
练习册系列答案
相关题目
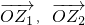（其中O为坐标原点），记向量
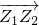所对应的复数为z，则z的共轭复数为________．