题目内容
若椭圆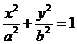 的焦点在x轴上,过点
的焦点在x轴上,过点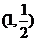 作圆
作圆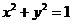 的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是 .
的切线,切点分别为A,B,直线AB恰好经过椭圆的右焦点和上顶点,则椭圆方程是 .
【答案】
答案: 解析:设过点(1,
解析:设过点(1, )的直线方程为:当斜率存在时,
)的直线方程为:当斜率存在时, ,
,
根据直线与圆相切,圆心(0,0)到直线的距离等于半径1可以得到k= ,直线与圆方程的联立可以得到切点的坐标(
,直线与圆方程的联立可以得到切点的坐标( ),当斜率不存在时,直线方程为:x=1,根据两点A:(1,0),B:(
),当斜率不存在时,直线方程为:x=1,根据两点A:(1,0),B:( )可以得到直线:2x+y-2=0,则与y轴的交点即为上顶点坐标(2,0)
)可以得到直线:2x+y-2=0,则与y轴的交点即为上顶点坐标(2,0) ,与x轴的交点即为焦点
,与x轴的交点即为焦点 ,根据公式
,根据公式 ,即椭圆方程为:
,即椭圆方程为:
(PS:此题可能算是填空题,比较纠结的一道,因为要理清思路,计算有些繁琐。但是,是不是就做不出来呢,不是的,在我们寒假题海班的时候讲过一道与此相似的题型,也就在理科教材第147页第23题。所以最纠结的一道高考题也不过如此,你们还怕什么?)

练习册系列答案
相关题目
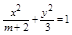 的焦点在x轴上,且离心率e=
的焦点在x轴上,且离心率e=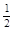 ,则m的值为( )
,则m的值为( )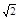 (B)2
(C)-
(B)2
(C)-