题目内容
已知P点是60°的二面角内一点，它到两个半平面的距离分别为2和3，则它到棱的距离是________．
分析：设垂足分别为A，B，先计算AB的长，再利用△PAB外接圆的直径为P到棱的距离，即可求得结论．
解答：
解：由题意，设垂足分别为A，B，则在△PAB中，PA=2，PB=3，∠APB=120°，∴AB2=4+9-2×2×3×cos∠APB=19
∴AB=
设P到棱的距离为l，则l=
=故答案为：
点评：本题考查点线距离的计算，解题的关键是正确运用余弦定理，正弦定理．
练习册系列答案
全能测控一本好卷系列答案
相关题目
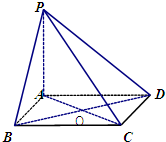（2012•上海二模）如图，在四棱锥P-ABCD中，已知AC与BD交于点O，PA⊥平面ABCD，底面ABCD是边长为4的菱形，∠BAD=12°，PA=4．
如图，点A、B是单位圆上的两点，A、B点分别在第一、二象限，点C是圆与x轴正半轴的交点，若∠COA=60°∠AOB=α，点B的坐标为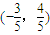
．
．
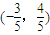