题目内容

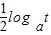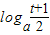设数a使a2+a-2＞0成立，t＞0，比较与的大小，结果为    ．
【答案】分析：由a2+a-2＞0，解得a＞1或a＜-2，由于a为底数，可得a＞1．利用已知和基本不等式可得，利用对数函数的单调性即可．
解答：解：由a2+a-2＞0，解得a＞1或a＜-2，
∵a为底数，∴a＞1．
又∵t＞0，∴，
∴．
故答案为．
点评：熟练掌握一元二次不等式的解法、基本不等式、对数函数的单调性等是解题的关键．
练习册系列答案
相关题目
设数a使a2+a-2＞0成立，t＞0，比较
1
2
log at与loga
t+1
2
的大小，结果为
1
2
log at≤loga
t+1
2
1
2
log at≤loga
t+1
2
．
（2008•杨浦区二模）（理）已知向量
a
=(x2+1，-x)，
b
=(1，2
n2+1
) （n为正整数），函数f(x)=
a 
• 
b 
，设f（x）在（0，+∞）上取最小值时的自变量x取值为an．
（1）求数列{an}的通项公式；
（2）已知数列{bn}，对任意正整数n，都有bn•（4an2-5）=1成立，设Sn为数列{bn}的前n项和，求
lim
n→∞
Sn；
（3）在点列A1（1，a1）、A2（2，a2）、A3（3，a3）、…、An（n，an）、…中是否存在两点Ai，Aj（i，j为正整数）使直线AiAj的斜率为1？若存在，则求出所有的数对（i，j）；若不存在，请你写出理由．
设数组A：{a1，a2，…，an}与数组B：{b1，b2，…，bn}，A与B中的元素不完全相同，分别从A、B中的n个元素中任取m（m≤n）个元素作和，各得Cnm个和．若由A得到的Cnm个和与由B得到的Cnm个和恰好完全相同，则称数组A与B是n元中取m的全等和数组，简记为DHnm数组．
（1）判断数组A：{5，15，25，45}与B：{0，20，30，40}是否为DH42数组？
（2）若数组A：{a1，a2，…，an}与数组B：{b1，b2，…，bn}是DHnm数组（m≤n），求证：数组A与B一定是DHnn数组
（3）给定数组A：{a1，a2，a3，a4}，其中a1≤a2≤a3≤a4，问是否存在数组B，使得数组A与B为DH42数组？若存在，则求出数组B；若不存在，请说明理由．
设数a使a2+a-2＞0成立，t＞0，比较
1
2
log at与loga
t+1
2
的大小，结果为______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网