题目内容
在一次抽奖活动中,有a、b、c、d、e、f 共6人获得抽奖的机会。抽奖规则如下:主办方先从6人中随机抽取两人均获一等奖,再从余下的4人中随机抽取1人获二等奖,最后还从这4人中随机抽取1人获三等奖。
(Ⅰ)求a能获一等奖的概率;
(Ⅱ)若a、b已获一等奖,求c能获奖的概率。
解:(Ⅰ)设“a能获一等奖”为事件A,
事件A等价于事件“从6人中随机取抽两人,能抽到a”.从6人中随机抽取两人的基本事件有(a、b)、(a、c)、(a、d)、(a、e)、(a、f)、(b、c)、(b、d)、(b、e)、(b、f)、(c、d)、(c、e)、(c、f)、(d、e)、(d、f)、(e、f)15个,
包含a的有5个,所以,P(A)=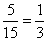 ,
,
答: a能获一等奖的概率为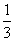 .
.
(Ⅱ)设“若a、b已获一等奖,c能获奖”为事件B,
a、b已获一等奖,余下的四个人中,获奖的基本事件有(c,c)、(c、d)、(c、e)、(c、f)、(d,c)、(d、d)、(d、e)、(d、f)、(e,c)、(e、d)、(e、e)、(e、f)、(f,c)、(f、d)、(f、e)、(f、f)16个,
其中含有c的有7种,所以,P(B)=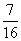 ,
,
答: 若a、b已获一等奖,c能获奖的概率为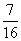 .
.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
 的各项均为正整数,且
的各项均为正整数,且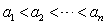 ,
,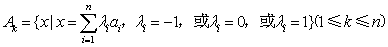 。
。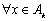 ,存在唯一一组
,存在唯一一组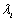 (
(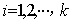 )使
)使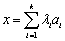 成立,则称数列
成立,则称数列 ,且对于任意
,且对于任意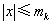 ,
,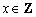 ,都有
,都有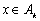 成立,则称数列
成立,则称数列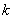 取最大值时
取最大值时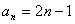 ,求集合
,求集合 ,并指出
,并指出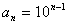 ,求证:数列
,求证:数列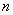 阶完备数列,并求出集合
阶完备数列,并求出集合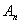 中所有元素的和
中所有元素的和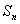 。
。 为虚数单位,复数
为虚数单位,复数 的虚部是
的虚部是 B.
B. C.
C. D .
D . 
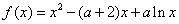 ,其中
,其中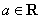 .
.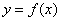 在点
在点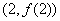 处的切线的斜率为
处的切线的斜率为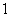 ,求
,求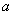 的值;
的值;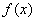 的单调区间.
的单调区间. ,则
,则 = 。
= 。 为等比数列
为等比数列 的前
的前 项和,
项和, ,则
,则
 :
: (
( 是参数)被圆C
是参数)被圆C :
:
 截得的弦长为 ;
截得的弦长为 ;  ,实轴长为4,则双曲线的方程是
,实轴长为4,则双曲线的方程是  上的函数
上的函数 满足
满足 且
且 时,
时, 则
则 ( )
( ) C.1 D.-
C.1 D.-