题目内容
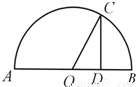
如图，AB是半圆O的直径，点C在半圆上，CD⊥AB于点D，且AD=3DB，设∠COD=θ，则tan2
=（ ）
A．
B．
C．4-2
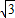
D．3
【答案】分析：由已知中AB是半圆O的直径，点C在半圆上，CD⊥AB于点D，且AD=3DB，我们可以设出圆的半径为R，进而根据射影定理求出CD的长，解三角形COD即可求出θ角，进而得到答案．
解答：解：设半径为R，
则AD=
R，BD=
，
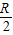由射影定理得：
CD2=AD•BD
则CD=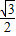
R，
从而θ=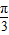
，
故tan2
=
，
故选A．
点评：本题考查的知识点是直角三角形的射影定理，其中根据射影定理求出CD的长，解三角形COD即可求出θ角，是解答本题的关键
解答：解：设半径为R，
则AD=
R，BD=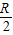，由射影定理得：
CD2=AD•BD
则CD=
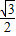R，从而θ=
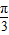，故tan2
=，故选A．
点评：本题考查的知识点是直角三角形的射影定理，其中根据射影定理求出CD的长，解三角形COD即可求出θ角，是解答本题的关键
练习册系列答案
备战中考寒假系列答案
相关题目
如图，AB是半圆O的直径，C是半圆O上异于A，B的点，CD⊥AB，垂足为D，已知AD=2，
21、选做题：
（2007•深圳一模）如图，AB是半圆O的直径，C在半圆上，CD⊥AB于D，且AD=3DB，设∠COD=θ，则
（2012•江苏一模）选做题
（1）（几何证明选讲）如图，AB是半圆O的直径，点C在半圆上，CD⊥AB，垂足为D，且AD=5DB，设∠COD=θ，则tanθ的值为