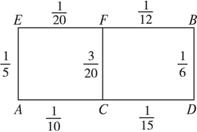
题目内容
某先生居住城镇的A处,准备开车到单位B上班。若该路段生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图。(如图A→C→D算作两个路段:路段AC发生堵车事件的概率为![]() ,路段CD发生堵车事件的概率为
,路段CD发生堵车事件的概率为![]() 。)
。)
(1)请你为其选择一条由A到B的路线,使得途中发生堵车事件的概率最小;
(2)若记路线A→C→F→B中遇到堵车次数为随机变量![]() ,求
,求![]() 的数学期望E
的数学期望E![]() 。
。

解:(1)路线A→E→F→B途中堵车概率为![]() ;
;
路线A→E→F→D→B途中堵车的概率为![]()
路线A→C→D→B途中堵车概率为![]()
路线A→C→F→B途中堵车概率为![]()
所以选择路线A→C→F→B途中发生堵车的概率最小
(2)解法一:由题意,![]() 可能取值为0,1,2,3 。
可能取值为0,1,2,3 。
P (![]() = 0) =
= 0) =![]()
P (![]() = 1) =
= 1) =![]()
P (![]() = 2) =
= 2) =![]()
P (![]() = 3) =
= 3) =![]()
E![]() = 0×P (
= 0×P (![]() = 0) + 1×P (
= 0) + 1×P (![]() = 1) +2×P (
= 1) +2×P (![]() = 2) + 3×P (
= 2) + 3×P (![]() = 3)
= 3)
=0×![]() +1×
+1×![]() +2×
+2×![]() +3×
+3×![]() =
=![]()
解法二:设![]() 1表示路线AC中遇到的堵车次数;
1表示路线AC中遇到的堵车次数;
![]() 2表示路线CF中遇到的堵车次数;
2表示路线CF中遇到的堵车次数;
![]() 3表示路线FB中遇到的堵车次数;
3表示路线FB中遇到的堵车次数;
则![]() =
=![]() 1+
1+![]() 2 +
2 +![]() 3 。∵E
3 。∵E![]() 1 =
1 =![]() , E
, E![]() 2 =
2 =![]() , E
, E![]() 3 =
3 =![]()
∴E![]() = E (
= E (![]() 1+
1+![]() 2 +
2 +![]() 3 ) = E
3 ) = E![]() 1+E
1+E![]() 2 +E
2 +E![]() 3 =
3 =![]() +
+![]() +
+![]() =
=![]()

练习册系列答案
相关题目
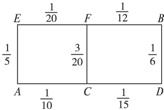 某先生居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如如图所示.(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为
某先生居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如如图所示.(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为 某先生居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率,如图.( 例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为
某先生居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率,如图.( 例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为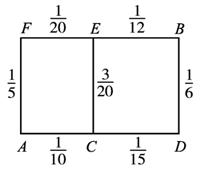
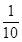 ,路段CD发生堵车事件的概率为115).
,路段CD发生堵车事件的概率为115).