Question

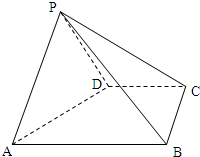（2011•延庆县一模）如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AB∥CD，∠DAB=60°，AB=AD=2CD，且三角形PAD为等腰△，PA=PD．
（Ⅰ）求证AD⊥PB；
（Ⅱ）线段AP上是否存在点M，使得MD∥平面PBC？
并说明理由．

Answer 1

分析：（1）由题意取AD的中点G，连接PG、GB、BD，因△PAD是等腰直角三角形，所以PG⊥AD，再由AB=AD，且∠DAB=60°得BG⊥AD，证出AD⊥平面PGB，即AD⊥PB；
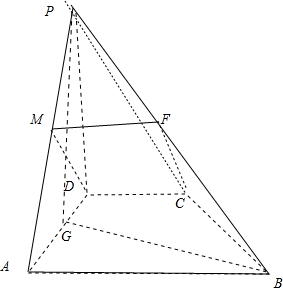
（2）考虑M为AP的中点，由题意取PB的中点F，连接MF、CF，由中位线和题意证出CDMF是平行四边形，得到DM∥CF，由线面平行的判定定理得DM∥平面PCB．

解答：解：（1）取AD的中点G，连接PG、GB、BD
∵PA=PD，
∴PG⊥AD．（2分）
∵AB=AD，且∠DAB=60°，
∴△ABD是正三角形，BG⊥AD，又PG∩BG=G
∴AD⊥平面PGB．
∴AD⊥PB．（6分）
（2）当M为PA的中点时，取PB的中点F，连接MF、CF，
∵M、F分别为PA、PB的中点，
∴MF∥AB，且MF=

1

2

AB．
∵四边形ABCD是直角梯形，AB∥CD且AB=2CD，
∴MF∥CD且MF=CD．（10分）
∴四边形CDMF是平行四边形．
∴DM∥CF．
∵CF?平面PCB，DM?平面PCB
∴DM∥平面PCB．（12分）

点评：本题主要考查了线面垂直和平行的判定定理的应用，主要用了中位线和等腰三角形的中线证明线线平行和垂直．