题目内容
【题目】(1)若数列![]() 的前n项和
的前n项和![]() ,求数列
,求数列![]() 的通项公式
的通项公式![]() .
.
(2)若数列![]() 的前n项和
的前n项和![]() ,证明
,证明![]() 为等比数列.
为等比数列.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)应用 ![]() (n
(n![]() ) 求解,再验证
) 求解,再验证![]() ,进而列出数列
,进而列出数列![]() 的通项公式
的通项公式![]() .
.
(2)应用 ![]() (n
(n![]() ) ,求得
) ,求得![]() 与bn-1的关系,进而证明
与bn-1的关系,进而证明 ![]() 为等比数列.
为等比数列.
(1) 当n≥2时,an=Sn-Sn-1=3n2-2n+1-[3(n-1)2-2(n-1)+1]=6n-5,
当n=1时,a1=S1=3×12-2×1+1=2;
显然当n=1时,不满足上式.
故数列的通项公式为![]()
(2)证明:由Tn=![]() bn+
bn+![]() ,得当n≥2时,Tn-1=
,得当n≥2时,Tn-1=![]() bn-1+
bn-1+![]() ,
,
两式相减,得bn=![]() bn-
bn-![]() bn-1,
bn-1,
∴当n≥2时,bn=-2bn-1,
又n=1时,T1=b1=![]() b1+
b1+![]() ,∴b1=1,
,∴b1=1,
∴bn=(-2)n-1.即![]() 为b1=1,公比q=-2的等比数列.
为b1=1,公比q=-2的等比数列.

练习册系列答案
相关题目
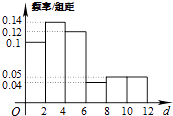
【题目】某公司共有职工1500人,其中男职工1050人,女职工450人.为调查该公司职工每周平均上网的时间,采用分层抽样的方法,收集了300名职工每周平均上网时间的样本数据(单位:小时)

男职工 | 女职工 | 总计 | |
每周平均上网时间不超过4个小时 | |||
每周平均上网时间超过4个小时 | 70 | ||
总计 | 300 |
(Ⅰ)应收集多少名女职工样本数据?
(Ⅱ)根据这300个样本数据,得到职工每周平均上网时间的频率分布直方图(如图所示),其中样本数据分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .试估计该公司职工每周平均上网时间超过4小时的概率是多少?
.试估计该公司职工每周平均上网时间超过4小时的概率是多少?
(Ⅲ)在样本数据中,有70名女职工的每周平均上网时间超过4个小时.请将每周平均上网时间与性别的![]() 列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”
列联表补充完整,并判断是否有95%的把握认为“该公司职工的每周平均上网时间与性别有关”