题目内容
若函数
在区间
内单调递增，则a的取值范围是 （ ） A．
B． 
C．
D．
B
解析：y=logat，t=x3－ax＞0，－＜x＜0或x＞，t′=3x2－a=0，x=±.
x | （－ | － | （－ | （ |
t′ | + | 0 | － | + |
t | 单增 | 极小值 | 单减 | 单增 |
－0）
+∞）当a＞1时，y=logat单增.
∴y=loga（x3－ax）的单增区间是（－
，－
）∪（
，+∞）（a＞0）
与y=loga（x3－ax）在（－
，0）内单增矛盾.
当0＜a＜1时，y=logat单减，
∴y=loga（x3－ax）的单增区间是（－
，0）.
又y=loga（x3－ax）在（－
，0）内单增，
∴（－
，0）
（－
，0）.∴－
≤－
.
∴a≥
.又0＜a＜1，∴
≤a＜1.故选B.
练习册系列答案
相关题目
的两条切线PM、PN，切点
时，求函数
的单调递均区间；
，试求函数
，在区间
内总存在
成立，求m的最大值.已知函数
，（
），
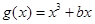
（1）若曲线
与曲线
在它们的交点（1，c）处具有公共切线，求a,b的值
（2）当
时，若函数
的单调区间，并求其在区间（-∞，-1）上的最大值。
【解析】（1）
，
∵曲线与曲线在它们的交点（1，c）处具有公共切线
∴
，
∴
（2）令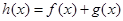
，当
时，
令
，得
时，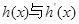
的情况如下：
|
x |
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
|
|
|
|
所以函数
的单调递增区间为
，
，单调递减区间为
当
，即
时，函数在区间
上单调递增，在区间上的最大值为
，
当
且
，即
时，函数在区间内单调递增，在区间
上单调递减，在区间上的最大值为
当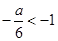
，即a>6时，函数在区间内单调递赠，在区间内单调递减，在区间
上单调递增。又因为
所以在区间上的最大值为。