Question

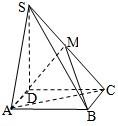四棱锥S-ABCD中，底面ABCD为矩形，平面SDC⊥底面ABCD，AD=

2

，DC=SD=2，SC=2

2

，点M是侧棱SC的中点．
（Ⅰ）求证：SD⊥平面ABCD；
（Ⅱ）求二面角C-AM-B的大小．

Answer 1

分析：（Ⅰ）欲证SD⊥平面ABCD，可根据面面垂直的性质可知只需证明平面SDC⊥底面ABCD，由勾股定理的逆定理知，SD⊥DC，满足面面垂直的判定定理的条件；
（Ⅱ）以D为坐标原点，以DA为x轴，DC为y轴，DS为z轴，建系D-xyz，然后求出平面CAM的一个法向量和平面AMB的一个法向量，求出两法向量所成角即为二面角C-AM-B的平面角．

解答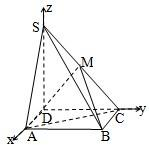：证明：（Ⅰ）因为DC=SD=2，SC=2

2

，由勾股定理的逆定理知，SD⊥DC，又平面SDC⊥底面ABCD于DC，SD?平面SDC，
所以，SD⊥平面ABCD．
解：（Ⅱ）由（Ⅰ）知，SD⊥DCSD⊥AD，又AD⊥DC，建系D-xyz．
于是，A(

2

，0，0)，C（0，2，0），S（0，0，2），M（0，1，1），

AM

=(-

2

，1，1)，

AC

=(-

2

，2，0)，
设

n1

=(x，y，z)为平面CAM的一个法向量，
则

- 2 x+y+z=0 - 2 x+2y=0

，得

n1

=(

2

，1，1)
又

AB

=(0，2，0)，设

n2

=(x，y，z)为平面AMB的一个法向量，
则

y=0 - 2 x+y+z=0

，得

n2

=(1，0，

2

)
因为cos＜

n1

，

n2

＞=

2 + 2

4× 3

=

6

6

，所以二面角C-AM-B为：arccos

6

6

点评：本题主要考查了线面垂直的判定，以及二面角及其平面角等有关知识，考查空间想象能力和思维能力，应用向量知识解决立体几何问题的能力．