题目内容
某公司为确定下一年度 投入某种产品的宣传费,需了解年宣传 费x(单位:千元)对年销量y(单位:t)和年利润z(单位:千元)的影. 对近8年的年宣传费xi和年销售量
 yi(i =1,2,···,8)数据作了初步处理得到下面的散点图及一些统计量的值.
yi(i =1,2,···,8)数据作了初步处理得到下面的散点图及一些统计量的值.
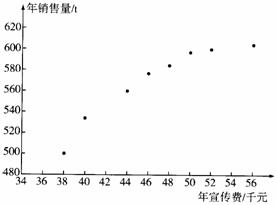
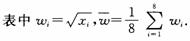
(Ⅰ)根据散点图判断,y=a+bx与y=c+d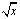 哪一个适宜作为年销售量y关于年宣传费
哪一个适宜作为年销售量y关于年宣传费
x的回归方程类型?(给出判断即可,不必说明理由)
(Ⅱ)根据(Ⅰ)的判断结果及表中数据,建立y关于x的回归方程;
(Ⅲ)已知这种产品的年利润z与x、y的关系为z=0.2y-x. 根据(Ⅱ)的结果回答下列问题:
(i)年宣传费x=49时,年销售量及年利润的预报值是多少?
(ii)年宣传费x为何值时,年利润的预报值最大?
附:对于一组数据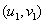 ,
,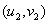 ,… ,
,… , , 其回归直线
, 其回归直线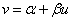 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为: 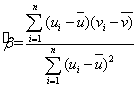 ,
,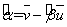 .
.
解:(Ⅰ)由散点图可以判断, 适宜作为年销售量
适宜作为年销售量 关于年宣传费
关于年宣传费 的回归方程类型. ………………………………………………2分
的回归方程类型. ………………………………………………2分
(Ⅱ)令 ,先建立
,先建立 关于
关于 的线性回归方程.
的线性回归方程.
由于  ,
,
 ,
,
所以 关于
关于 的线性回归方程为
的线性回归方程为 ,
,
因此 关于
关于 的线性回归方程为
的线性回归方程为 . ………………………6分
. ………………………6分
(Ⅲ)(i)由(Ⅱ)知,当 时,
时,
年销量 的预报值
的预报值 ,
,
年利润 的预报值
的预报值 . ………………………8分
. ………………………8分
(ii)根据(Ⅱ)的结果知,年利润 的预报值
的预报值
 .
.
所以当 ,即
,即 时,
时, 取得最大值.
取得最大值.
故年宣传费为46.24千元时,年利润的预报值最大. ………………………10分

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案
相关题目
 的前
的前 项和为
项和为 ,且
,且 ,
, .
. 的前
的前 ,求
,求 的值.
的值. 定义在R上的奇函数,当
定义在R上的奇函数,当 时,
时,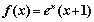 ,给出下列命题:
,给出下列命题: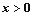 时,
时,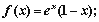 ②函数
②函数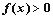 的解集为
的解集为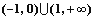 ④
④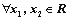 ,都有
,都有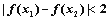
 服从正态分布
服从正态分布 , 若
, 若 , 则
, 则
 中,
中,  ,则
,则 等于 ( )
等于 ( ) B.
B.  C.
C.  D.
D. 
 和
和 ,定义
,定义 ;若向量
;若向量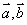 满足
满足 ,
, 与
与 的夹角
的夹角 ,且
,且 都在集合
都在集合 中,
中, ( )
( ) B.
B.  C.
C.  D.
D. 
 的值为
的值为 ,则输出的
,则输出的 的值为( )A.22 B.16 C.15 D.11
的值为( )A.22 B.16 C.15 D.11 
 的定义域为
的定义域为 集合
集合

