题目内容
7.设函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上单调递增,则满足不等式f(1)<f(lg$\frac{x}{10}$)的x的取值范围是(0,1)∪(100,+∞).分析 根据函数是偶函数,把不等式转化成f(1)<f(|lg$\frac{x}{10}$|),就可以利用函数在区间[0,+∞)上单调递增转化成一般的不等式进行求解.
解答 解:∵函数f(x)是定义在R上的偶函数,
∴f(1)<f(lg$\frac{x}{10}$)=f(|lg$\frac{x}{10}$|)
∵函数f(x)在区间[0,+∞)上单调递增,
∴|lg$\frac{x}{10}$|>1,即lg$\frac{x}{10}$>1或lg$\frac{x}{10}$<-1
解得:x>100或0<x<1
所以满足不等式f(1)<f(lg$\frac{x}{10}$)的x的取值范围是(0,1)∪(100,+∞).
故答案为:(0,1)∪(100,+∞).
点评 本题考查了利用函数的奇偶性和单调性解抽象不等式,解题的关键是利用函数的奇偶性把自变量转化到同一个单调区间上,还要注意函数的定义域.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
15.若$π<α<\frac{3π}{2}$,$\sqrt{\frac{1-cosα}{1+cosα}}+\sqrt{\frac{1+cosα}{1-cosα}}$的化简结果为( )
| A. | $\frac{2}{tanα}$ | B. | -$\frac{2}{tanα}$ | C. | $\frac{2}{sinα}$ | D. | -$\frac{2}{sinα}$ |
2.如果棱长为2$\sqrt{2}$的正四面体的顶点都在一个球面上,那么这个球的表面积是( )
| A. | 8π | B. | 12π | C. | 16π | D. | 20π |
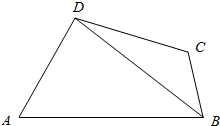 如图,在四边形ABCD中,AB=8,BC=3,CD=5,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.
如图,在四边形ABCD中,AB=8,BC=3,CD=5,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.


