题目内容
已知函数 .
.
(1)若 的定义域和值域均是
的定义域和值域均是 ,求实数
,求实数 的值;
的值;
(2)若 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的 ,都有
,都有 ,求实数
,求实数 的取值范围;
的取值范围;
(3)若 ,且对任意的
,且对任意的 ,都存在
,都存在 ,使得
,使得 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(1)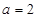 ;(2)
;(2)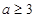 ;(3)
;(3) .
.
解析试题分析:(1)先利用二次函数的性质确定函数 的单调递减区间为
的单调递减区间为 ,故
,故 在
在 单调递减,然后由定义域与值域列出等式关系,从而求解即可;(2)由(1)可知
单调递减,然后由定义域与值域列出等式关系,从而求解即可;(2)由(1)可知 ,初步确定
,初步确定 的取值范围
的取值范围 ,然后确定
,然后确定 时函数
时函数 的最大值
的最大值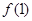 ,从中求解不等式组
,从中求解不等式组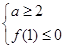 即可;(3)将“对任意的
即可;(3)将“对任意的 ,都存在
,都存在 ,使得
,使得 成立”转化为
成立”转化为 时,
时,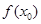 的值域包含了
的值域包含了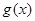 在
在 的值域,然后进行分别求
的值域,然后进行分别求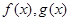 在
在 的值域,从集合间的包含关系即可求出
的值域,从集合间的包含关系即可求出 的取值范围.
的取值范围.
试题解析:(1)∵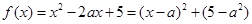
∴ 在
在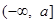 上单调递减,又
上单调递减,又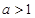 ,∴
,∴ 在
在 上单调递减,
上单调递减,
∴ ,∴
,∴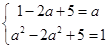 ,∴
,∴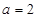 4分
4分
(2)∵ 在区间
在区间 上是减函数,∴
上是减函数,∴ ,∴
,∴
∴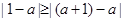 ,
,
∴ 时,
时,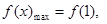
又∵对任意的 ,都有
,都有 ,
,
∴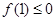 ,即
,即 ,也就是
,也就是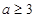
综上可知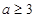 8分
8分
(3)∵ 在
在 上递增,
上递增, 在
在 上递减,
上递减,
当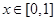 时,
时,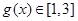 ,
,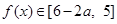
∵对任意的 ,都存在
,都存在 ,使得
,使得 成立
成立
∴
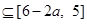
∴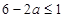 ,所以
,所以 13分
13分
考点:1.二次函数图像与性质;2.函数的单调性;3.函数与方程的问题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
我国是水资源较贫乏的国家之一,各地采用价格调控等手段来达到节约用水的目的,某市每户每月用水收费办法是:水费=基本费+超额费+定额损耗费.且有如下两条规定:
①若每月用水量不超过最低限量 立方米,只付基本费10元加上定额损耗费2元;
立方米,只付基本费10元加上定额损耗费2元;
②若用水量超过 立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付
立方米时,除了付以上同样的基本费和定额损耗费外,超过部分每立方米加付 元的超额费.
元的超额费.
解答以下问题:(1)写出每月水费 (元)与用水量
(元)与用水量 (立方米)的函数关系式;
(立方米)的函数关系式;
(2)若该市某家庭今年一季度每月的用水量和支付的费用如下表所示:
| 月份 | 用水量(立方米) | 水费(元) |
| 一 | 5 | 17 |
| 二 | 6 | 22 |
| 三 |  | 12 |
试判断该家庭今年一、二、三各月份的用水量是否超过最低限量,并求
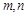 的值.
的值.  的定义域是
的定义域是 ,对于任意的
,对于任意的 ,有
,有 ,且当
,且当 时,
时, .
. 的值;
的值; 为增函数;
为增函数; 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 对任意实数
对任意实数 均有
均有 ,且当
,且当 时,
时,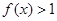 .
.
 时,解不等式
时,解不等式
 (其中
(其中 ,a为正常数).已知生产该产品还需投入成本10+2P万元(不含促销费用),产品的销售价格定为
,a为正常数).已知生产该产品还需投入成本10+2P万元(不含促销费用),产品的销售价格定为 元/件.
元/件. .
. ,试判断
,试判断 在定义域内的单调性;
在定义域内的单调性; 时,若
时,若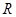 上有
上有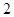 个零点,求
个零点,求 的取值范围.
的取值范围. 在[
在[ ,+∞)上的单调性.
,+∞)上的单调性. 对任意
对任意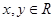 ,都有
,都有 ,当
,当 时,
时,
 时
时  ,
,
 .
. ,求f(α)的值.
,求f(α)的值.