题目内容
 有一批材料可以围成200米长的围墙,现用此材料在一边靠墙的地方围成一块矩形场地(如图),且内部用此材料隔成三个面积相等的矩形,则围成的矩形场地的最大面积为( )
有一批材料可以围成200米长的围墙,现用此材料在一边靠墙的地方围成一块矩形场地(如图),且内部用此材料隔成三个面积相等的矩形,则围成的矩形场地的最大面积为( )分析:设每个小矩形长为x,宽为y,则依题意可知4x+3y=200,代入矩形的面积公式,根据基本不等式求得围成矩形面积的最大值.
解答:解:设每个小矩形长为x,宽为y,则4x+3y=200,
S=3xy=x(200-4x)=4x(50-x)≤4(
)2=2500,
∴当且仅当x=50-x,即x=25时,Smax=2500(m2)
故选C.
S=3xy=x(200-4x)=4x(50-x)≤4(
| x+50-x |
| 2 |
∴当且仅当x=50-x,即x=25时,Smax=2500(m2)
故选C.
点评:本题主要考查了函数的最值的应用.考查了学生分析问题和解决问题的能力.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
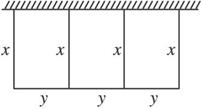
 有一批材料可以围成200米长的围墙,现用此材料在一边靠墙的地方围成一块矩形场地(如图),且内部用此材料隔成三个面积相等的矩形,则围成的矩形场地的最大面积为
有一批材料可以围成200米长的围墙,现用此材料在一边靠墙的地方围成一块矩形场地(如图),且内部用此材料隔成三个面积相等的矩形,则围成的矩形场地的最大面积为