题目内容
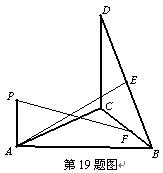
 如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.
如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.(Ⅰ)证明:AE⊥BC;
(Ⅱ)若点F是线段BC上的动点,设平面PFE与平面PBE所成的平面角大小为θ,当θ在[0,
 ]内取值时,直线PF与平面DBC所成的角为α,求tanα的取值范围.
]内取值时,直线PF与平面DBC所成的角为α,求tanα的取值范围.
【答案】分析:(I)取BC得中点M,连接EM,AM,根据题意证出MA、MB、ME两两互相垂直,从而以MA、MB、ME为x,y,z轴,建立如图所示空间直角坐标系.设AB=BC=AC=DC=2,可得A、B、C、D、E、P、M各点的坐标,从而算出向量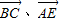 的坐标,计算它们的数量积得到0,即可证出AE⊥BC;
的坐标,计算它们的数量积得到0,即可证出AE⊥BC;
(II) 设F(0,y,0),且-1≤y≤1.利用垂直向量数量积为零的方法建立方程组,解出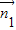 =(0,1,1)是平面PBE的一个法向量;同样的方法算出
=(0,1,1)是平面PBE的一个法向量;同样的方法算出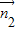 =(0,y,-1)是平面PEF的一个法向量,利用空间向量的夹角公式结合θ∈[0,
=(0,y,-1)是平面PEF的一个法向量,利用空间向量的夹角公式结合θ∈[0,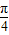 ]建立不等式关系,算出0≤y≤1.而PF与平面DBC所成的角为α,满足
]建立不等式关系,算出0≤y≤1.而PF与平面DBC所成的角为α,满足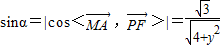 ,用同角三角函数的基本关系算出tanα=
,用同角三角函数的基本关系算出tanα=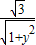 ,结合0≤y≤1,可得tanα∈[
,结合0≤y≤1,可得tanα∈[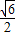 ,3].
,3].
解答:解:取BC得中点M,连接EM,AM,
∵直角△BCD中,DC=BC,∴DC⊥BC
∵平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,∴DC⊥平面ABC
∵△BCD中,EM是中位线,∴EM∥DC,可得EM⊥平面ABC
∵AM是等边△ABC的中线,∴AM⊥BC
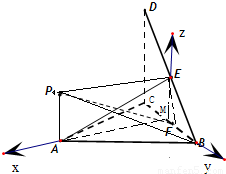
分别以MA、MB、ME为x,y,z轴,建立如图所示的空间直角坐标系.
设AB=BC=AC=DC=2,则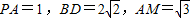
可得M(0,0,0),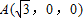 ,B(0,1,0),C(0,-1,0),
,B(0,1,0),C(0,-1,0),
D(0,-1,2),E(0,0,1),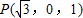 ,
,
(Ⅰ)∵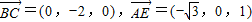 ,
,
∴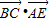 =0×
=0×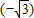 +(-2)×0+0×1=0
+(-2)×0+0×1=0
由此可得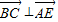 ,即AE⊥BC;------------------(6分)
,即AE⊥BC;------------------(6分)
(Ⅱ) 设F(0,y,0),且-1≤y≤1,
平面PBE的一个法向量为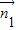 =(x1,y1,z1),
=(x1,y1,z1),
平面PEF的一个法向量为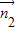 =(x2,y2,z2),又有:
=(x2,y2,z2),又有: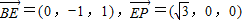 ,
,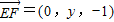
∴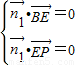 即
即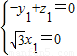 ,
,
取y1=1,得x1=0,z1=1,可得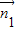 =(0,1,1)
=(0,1,1)
又∵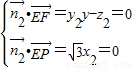 ,∴取y2=1,得x2=0,z2=y,可得
,∴取y2=1,得x2=0,z2=y,可得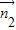 =(0,1,y),
=(0,1,y),
又∵cos<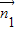 ,
,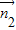 >=|cosθ|∈[
>=|cosθ|∈[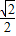 ,1],θ∈[0,
,1],θ∈[0,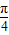 ]
]
∴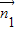 •
•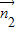 =|
=|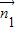 |•|
|•|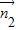 |cos<
|cos<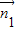 ,
,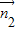 >,可得
>,可得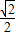 ≤
≤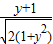 ≤1,解之得0≤y≤1,
≤1,解之得0≤y≤1,
又∵向量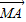 是平面DBC的一个法向量,且
是平面DBC的一个法向量,且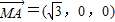 ,
,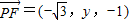 ,
,
且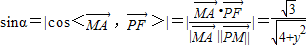
∴tanα=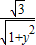 ,结合0≤y≤1,可得tanα∈[
,结合0≤y≤1,可得tanα∈[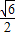 ,3]-------------------------------------(14分)
,3]-------------------------------------(14分)
点评:本题利用建立空间坐标系的方法证明了直线与直线垂直,并研究的平面与平面所成的角和直线与平面所成角的范围.着重考查了建系、设点、求向量坐标、建立方程组寻找法向量、利用空间向量夹角公式研究面面角和线面角等用解析法研究空间位置关系的一般步骤,属于中档题.
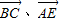 的坐标,计算它们的数量积得到0,即可证出AE⊥BC;
的坐标,计算它们的数量积得到0,即可证出AE⊥BC;(II) 设F(0,y,0),且-1≤y≤1.利用垂直向量数量积为零的方法建立方程组,解出
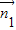 =(0,1,1)是平面PBE的一个法向量;同样的方法算出
=(0,1,1)是平面PBE的一个法向量;同样的方法算出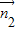 =(0,y,-1)是平面PEF的一个法向量,利用空间向量的夹角公式结合θ∈[0,
=(0,y,-1)是平面PEF的一个法向量,利用空间向量的夹角公式结合θ∈[0,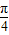 ]建立不等式关系,算出0≤y≤1.而PF与平面DBC所成的角为α,满足
]建立不等式关系,算出0≤y≤1.而PF与平面DBC所成的角为α,满足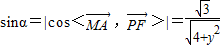 ,用同角三角函数的基本关系算出tanα=
,用同角三角函数的基本关系算出tanα=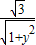 ,结合0≤y≤1,可得tanα∈[
,结合0≤y≤1,可得tanα∈[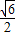 ,3].
,3].解答:解:取BC得中点M,连接EM,AM,
∵直角△BCD中,DC=BC,∴DC⊥BC
∵平面ABC⊥平面BCD,平面ABC∩平面BCD=BC,∴DC⊥平面ABC
∵△BCD中,EM是中位线,∴EM∥DC,可得EM⊥平面ABC
∵AM是等边△ABC的中线,∴AM⊥BC
分别以MA、MB、ME为x,y,z轴,建立如图所示的空间直角坐标系.
设AB=BC=AC=DC=2,则
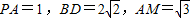
可得M(0,0,0),
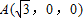 ,B(0,1,0),C(0,-1,0),
,B(0,1,0),C(0,-1,0),D(0,-1,2),E(0,0,1),
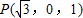 ,
,
(Ⅰ)∵
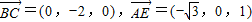 ,
,∴
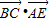 =0×
=0×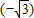 +(-2)×0+0×1=0
+(-2)×0+0×1=0由此可得
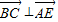 ,即AE⊥BC;------------------(6分)
,即AE⊥BC;------------------(6分)(Ⅱ) 设F(0,y,0),且-1≤y≤1,
平面PBE的一个法向量为
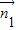 =(x1,y1,z1),
=(x1,y1,z1),平面PEF的一个法向量为
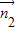 =(x2,y2,z2),又有:
=(x2,y2,z2),又有: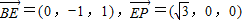 ,
,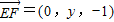
∴
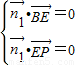 即
即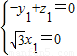 ,
,取y1=1,得x1=0,z1=1,可得
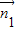 =(0,1,1)
=(0,1,1)又∵
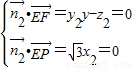 ,∴取y2=1,得x2=0,z2=y,可得
,∴取y2=1,得x2=0,z2=y,可得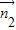 =(0,1,y),
=(0,1,y),又∵cos<
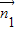 ,
,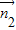 >=|cosθ|∈[
>=|cosθ|∈[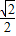 ,1],θ∈[0,
,1],θ∈[0,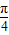 ]
]∴
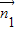 •
•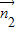 =|
=|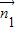 |•|
|•|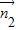 |cos<
|cos<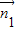 ,
,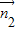 >,可得
>,可得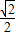 ≤
≤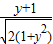 ≤1,解之得0≤y≤1,
≤1,解之得0≤y≤1,又∵向量
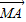 是平面DBC的一个法向量,且
是平面DBC的一个法向量,且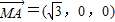 ,
,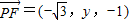 ,
,且
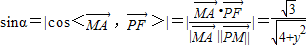
∴tanα=
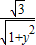 ,结合0≤y≤1,可得tanα∈[
,结合0≤y≤1,可得tanα∈[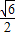 ,3]-------------------------------------(14分)
,3]-------------------------------------(14分)点评:本题利用建立空间坐标系的方法证明了直线与直线垂直,并研究的平面与平面所成的角和直线与平面所成角的范围.着重考查了建系、设点、求向量坐标、建立方程组寻找法向量、利用空间向量夹角公式研究面面角和线面角等用解析法研究空间位置关系的一般步骤,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
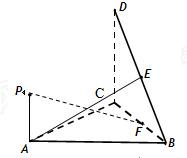 如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.
如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.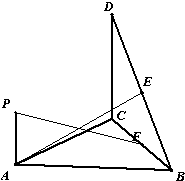 如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E、F分别为DB、CB的中点,
如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E、F分别为DB、CB的中点, (2010•温州一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,为DB的中点,
(2010•温州一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,为DB的中点,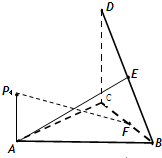 (2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点.
(2012•汕头一模)如图,直角△BCD所在的平面垂直于正△ABC所在的平面,PA⊥平面ABC,DC=BC=2PA,E为DB的中点. ,
, 为DB的中点,
为DB的中点, ,若存在,试确定点F的位置,若不存在,说明理由.
,若存在,试确定点F的位置,若不存在,说明理由.