题目内容
16．设α∈R，函数f（x）=（$\frac{1}{3}$）x-1-a的图象一定经过（ ）| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
分析 根据指数函数的性质求出函数的取值范围即可．
解答 解：∵f（x）=（$\frac{1}{3}$）x-1-a为减函数，
∴当a=0时，函数f（x）＞0，则函数不经过第四象限，
若a=3，则f（0）=1-1=0，此时函数不经过第三象限，
若a＜3，则f（0）=1-a＜0，则函数不经过第一象限，
故函数f（x）的图象一定经过第二象限，
故选：B
点评 本题主要考查指数函数的图象和性质，根据条件进行排除是解决本题的关键．
练习册系列答案
芝麻开花课程新体验系列答案
相关题目
6．已知$cosα=-\frac{3}{5}，α∈（0，π）$，则tanα=（ ）
| A． | $\frac{4}{3}$ | B． | $-\frac{4}{3}$ | C． | $±\frac{4}{3}$ | D． | $±\frac{3}{4}$ |
7．由6本不同的书，分成4份，两份各1本，其余两份各2本，则不同的分法有（ ）
| A． | 30 | B． | 45 | C． | 180 | D． | 720 |
11．sin160°sin10°-cos20°cos10°的值是（ ）
| A． | -$\frac{\sqrt{3}}{2}$ | B． | -$\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{\sqrt{3}}{2}$ |
8．已知函数f（x）=ax（a＞0，a≠1），其导函数为f′（x），满足f（x）＜f′（x）对于任意实数x恒成立，则（ ）
| A． | f（1）＞e，f（2012）＞e2012 | B． | f（1）＞e，f（2012）＜e2012 | ||
| C． | f（1）＜e，f（2012）＞e2012 | D． | f（1）＜e，f（2012）＜e2012 |
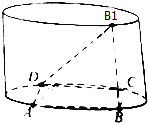如图，圆柱底面直径为10，母线BB1=6，矩形ABCD内接于圆柱的下底面，BC=6，求直线DB1与BC所成角的大小．（结果用反三角函教值表示）