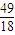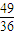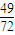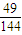题目内容
曲线y= x3+
x3+ x2在点T(1,
x2在点T(1, )处的切线与两坐标轴围成的三角形的面积为( )
)处的切线与两坐标轴围成的三角形的面积为( )A.
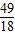
B.
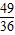
C.
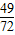
D.
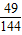
【答案】分析:由题意易知,点T为切点,故根据导数的几何意义,可得切线的方程,从而求出切线与两坐标轴的截距,故切线与两坐标轴围成的三角形的面积可求.
解答:解:由题意易知,点T为切点,
∵f′(1)=2,
∴切线方程为:y=2x- ,
,
∴它在两坐标轴的截距分别为 ,-
,- ,
,
∴与两坐标轴围成的三角形面积S= ×
× ×|-
×|- |=
|= .
.
故选D.
点评:本题考查了导数的几何意义,主要用于解决切线问题.
解答:解:由题意易知,点T为切点,
∵f′(1)=2,
∴切线方程为:y=2x-
 ,
,∴它在两坐标轴的截距分别为
 ,-
,- ,
,∴与两坐标轴围成的三角形面积S=
 ×
× ×|-
×|- |=
|= .
.故选D.
点评:本题考查了导数的几何意义,主要用于解决切线问题.

练习册系列答案
相关题目
 x3+
x3+ x2在点T(1,
x2在点T(1, )处的切线与两坐标轴围成的三角形的面积为( )
)处的切线与两坐标轴围成的三角形的面积为( )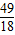

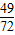
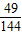
 x3+
x3+ x2在点T(1,
x2在点T(1, )处的切线与两坐标轴围成的三角形的面积为( )
)处的切线与两坐标轴围成的三角形的面积为( )