题目内容
P是△ABC所在平面α外一点,O是点P在平面α内的射影.(1)若P点到△ABC的三个顶点等距离,那么O点是△ABC的什么心?
(2)若P点到△ABC的三边距离相等,且O点在△ABC的内部,那么O点是△ABC的什么心?
解析:(1)O点是△ABC的外心,如下图所示.
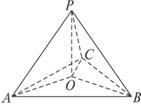
∵O是P点在α内的射影,
连结OA、OB、OC,则OA、OB、OC分别为PA、PB、PC在α内的射影.
又PA=PB=PC,
知OA=OB=OC,故O点是△ABC的外心.
(2)O点是△ABC的内心.如下图所示.
作OF⊥AC于F,OE⊥BC于E,OD⊥AB于D,
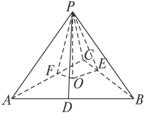
连结PF、PE、PD.
又PO⊥α于O,由三垂线定理,知
PF⊥AC于F,PE⊥BC于E,PD⊥AB于D.
故PF、PE、PD的长分别是P点到AC、BC、AB的距离,
则PF=PE=PD,从而OF=OE=OD,O点为△ABC的内心.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
设P是△ABC所在平面上一点,且
-
=
-
,若△ABC的面积为2,则△PBC面积为( )
| CA |
| CP |
| CP |
| CB |
A、
| ||
| B、1 | ||
| C、2 | ||
| D、4 |