题目内容
已知函数 的定义域为[-3,2],则该函数的值域为________.
的定义域为[-3,2],则该函数的值域为________.
[ ]
]
分析:由于x∈[-3,2],可得 ≤
≤ ≤8,令 t=
≤8,令 t= ,有y=t2-t+1=
,有y=t2-t+1=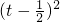 +
+ ,再利用二次函数的性质求出它的最值.
,再利用二次函数的性质求出它的最值.
解答:由于x∈[-3,2],∴ ≤
≤ ≤8,令 t=
≤8,令 t= ,
,
则有y=t2-t+1=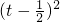 +
+ ,
,
故当t= 时,y有最小值为
时,y有最小值为 ,当t=8时,y有最大值为57,
,当t=8时,y有最大值为57,
故答案为[ ].
].
点评:本题主要考查指数型函数的性质以及应用,求二次函数在闭区间上的最值,属于中档题.
 ]
]分析:由于x∈[-3,2],可得
 ≤
≤ ≤8,令 t=
≤8,令 t= ,有y=t2-t+1=
,有y=t2-t+1=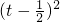 +
+ ,再利用二次函数的性质求出它的最值.
,再利用二次函数的性质求出它的最值.解答:由于x∈[-3,2],∴
 ≤
≤ ≤8,令 t=
≤8,令 t= ,
,则有y=t2-t+1=
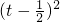 +
+ ,
,故当t=
 时,y有最小值为
时,y有最小值为 ,当t=8时,y有最大值为57,
,当t=8时,y有最大值为57,故答案为[
 ].
].点评:本题主要考查指数型函数的性质以及应用,求二次函数在闭区间上的最值,属于中档题.

练习册系列答案
相关题目
已知函数 的定义域为
的定义域为 ,部分对应值如下表。
,部分对应值如下表。 的导函数
的导函数 的图像如图所示。
的图像如图所示。
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|

下列关于函数 的命题:
的命题:
①函数 在
在 上是减函数;②如果当
上是减函数;②如果当 时,
时, 最大值是
最大值是 ,那么
,那么 的最大值为
的最大值为 ;③函数
;③函数 有
有 个零点,则
个零点,则 ;④已知
;④已知 是
是 的一个单调递减区间,则
的一个单调递减区间,则 的最大值为
的最大值为 。
。
其中真命题的个数是( )
A、4个 B、3个 C、2个 D、1个
 的定义域为
的定义域为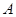 ,
,  ,且
,且 的真子集,求实数
的真子集,求实数 的取值范围.
的取值范围.




 的定义域为
的定义域为 ,且
,且 ,
, 为
为 ,
, 满足
满足 ,则
,则 的取值范围是
的取值范围是
 B.
B. C.
C. D.
D.