题目内容

在同一坐标系中,方程a2x2+b2y2=1与ax+by2=0(a＞b＞0)的曲线大致是(　　)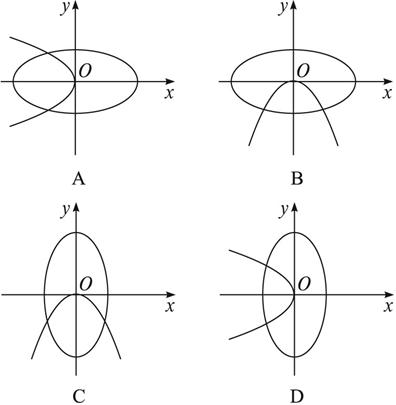

解法一:将方程a2x2+b2y2=1与ax+by2=0转化为标准方程因为a＞b＞0,因此

所以椭圆的焦点在y轴上,抛物线的开口向左.

解法二:将方程ax+by2=0中的y换成-y,其结果不变,

即说明ax+by2=0的图象关于x轴对称,排除B、C,又椭圆的焦点在y轴上,排除A.

答案:D

练习册系列答案
相关题目
12、方程mx+ny2=0与mx2+ny2=1（m＞0，n＞0，m≠n）表示的曲线在同一坐标系中的示意图可能为（　　）
下面有5个命题：
①函数y=sin4x-cos4x的最小正周期是π．
②终边在y轴上的角的集合是{α|α=
kπ
2
，k∈Z}．
③在同一坐标系中，函数y=sinx的图象和函数y=x的图象有三个公共点．
④函数y=sin(2x+
π
3
)图象的对称轴方程可能是x=
π
12
．
⑤函数y=sin(x-
π
2
)在[0，π]上是减函数．
其中，真命题的编号是
 
（写出所有真命题的编号）
在同一坐标系中，方程
x2
n2
+
y2
m2
=1与y2=-
m
n
x（m＞n＞0）的曲线大致是（　　）
给出下列四个命题，其中错误的命题有（　　）个．
（1）将函数y=sin(2x+
π
3
)的图象向右平移
π
3
个单位，得到函数y=sin2x的图象；
（2）函数y=sin2x+cos2x在x∈[0，
π
2
]上的单调递增区间是[0，
π
8
]；
（3）设A、B、C∈(0，
π
2
)且sinA-sinC=sinB，cosA+cosC=cosB，则B-A等于-
π
3
；
（4）方程sin2x+2sinx+a=0有解，则a的取值范围是[-3，1]．
（5）在同一坐标系中，函数y=sinx与函数y=
x
2
的图象有三个交点．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网