题目内容
 如图,在棱长为a正方体ABCD-A1B1C1D1中.
如图,在棱长为a正方体ABCD-A1B1C1D1中.(1)求异面直线AC与BC1所成的角;
(2)求三棱锥B1-A1BC1的体积.
分析:(1)在棱长为a正方体ABCD-A1B1C1D1中,由于AC和A1C1平行且相等,可得∠BC1A1即为异面直线AC与BC1所成的角.再由△BC1A1为等边三角形可得∠BC1A1=60°,由此可得结论.
(2)三棱锥B1-A1BC1的体积 即VB-A1B1C1=
•S△A1B1C1•BB1,运算求得结果.
(2)三棱锥B1-A1BC1的体积 即VB-A1B1C1=
| 1 |
| 3 |
解答:解:(1)在棱长为a正方体ABCD-A1B1C1D1中,AC和A1C1平行且相等,
故∠BC1A1即为异面直线AC与BC1所成的角.
再由△BC1A1为等边三角形可得∠BC1A1=60°,故异面直线AC与BC1所成的角为60°.
(2)三棱锥B1-A1BC1的体积 即VB-A1B1C1=
•S△A1B1C1•BB1=
(
a•a)a=
a3.
故∠BC1A1即为异面直线AC与BC1所成的角.
再由△BC1A1为等边三角形可得∠BC1A1=60°,故异面直线AC与BC1所成的角为60°.
(2)三棱锥B1-A1BC1的体积 即VB-A1B1C1=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
点评:本题主要考查求异面直线所成的角,求棱锥的体积,体现了转化的数学思想,属于中档题.

练习册系列答案
相关题目
 (2013•泉州模拟)如图,在棱长为1的正方体ABCD-A1B1C1D1的对角线AC1上任取一点P,以A为球心,AP为半径作一个球.设AP=x,记该球面与正方体表面的交线的长度和为f(x),则函数f(x)的图象最有可能的是( )
(2013•泉州模拟)如图,在棱长为1的正方体ABCD-A1B1C1D1的对角线AC1上任取一点P,以A为球心,AP为半径作一个球.设AP=x,记该球面与正方体表面的交线的长度和为f(x),则函数f(x)的图象最有可能的是( )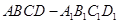 的对角线
的对角线 上任取一点P,以
上任取一点P,以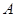 为球心,
为球心, 为半径作一个球.设
为半径作一个球.设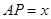 ,记该球面与正方体表面的交线的长度和为
,记该球面与正方体表面的交线的长度和为 ,则函数
,则函数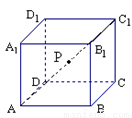

 内有一个内切球O,则过棱
内有一个内切球O,则过棱 和
和 的中点
的中点 、
、 的直线与球面交点为
的直线与球面交点为 、
、 ,则
,则 A.
A. B.
B. C.
C. D.
D. 
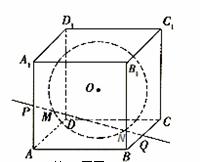 如图,在棱长为2的正方体
如图,在棱长为2的正方体 内有一个内切球O,则过棱
内有一个内切球O,则过棱 和
和 的中点
的中点 、
、 的直线与球面交点为
的直线与球面交点为 、
、 ,则
,则 B.
B.
 D.
D.
 如图,在棱长为2的正方体
如图,在棱长为2的正方体