题目内容
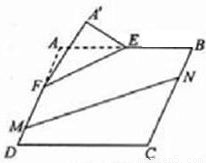
如图,在矩形ABCD中,点E,F分别在线段AB,AD上,AE=EB=AF= FD=4.沿直线EF将△AEF翻折成△A′EF,使平面A′EF⊥平面BEF.
FD=4.沿直线EF将△AEF翻折成△A′EF,使平面A′EF⊥平面BEF.(Ⅰ)求二面角A′-FD-C的余弦值;
(Ⅱ)点M,N分别在线段FD,BC上,若沿直线MN将四边形MNCD向上翻折,使C与A′重合,求线段FM的长.
【答案】分析:本题主要考查空间点、线、面位置关系,二面角等基础知识,空间向量的应用,同事考查空间想象能力和运算求解能力.
(1)取线段EF的中点H,连接A′H,因为A′E=A′F及H是EF的中点,所以A′H⊥EF,又因为平面A′EF⊥平面BEF.则我们可以以A的原点,以AE,AF,及平面ABCD的法向量为坐标轴,建立空间直角坐标系A-xyz,则锐二面角A′-FD-C的余弦值等于平面A′FD的法向量,与平面BEF的一个法向量夹角余弦值的绝对值.
(2)设FM=x,则M(4+x,0,0),因为翻折后,C与A重合,所以CM=A′M,根据空间两点之间距离公式,构造关于x的方程,解方程即可得到FM的长.
解答:解:(Ⅰ)取线段EF的中点H,连接A′H,因为A′E=A′F及H是EF的中点,所以A′H⊥EF,
又因为平面A′EF⊥平面BEF.
如图建立空间直角坐标系A-xyz
则A′(2,2,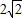 ),C(10,8,0),
),C(10,8,0),
F(4,0,0),D(10,0,0).
故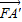 =(-2,2,2
=(-2,2,2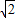 ),
),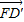 =(6,0,0).
=(6,0,0).
设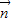 =(x,y,z)为平面A′FD的一个法向量,
=(x,y,z)为平面A′FD的一个法向量,
-2x+2y+2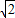 z=0
z=0
所以6x=0.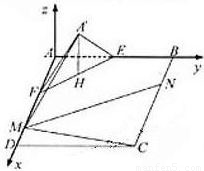
取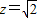 ,则
,则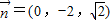 .
.
又平面BEF的一个法向量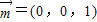 ,
,
故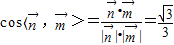 .
.
所以二面角的余弦值为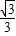
(Ⅱ)设FM=x,则M(4+x,0,0),
因为翻折后,C与A重合,所以CM=A′M,
故,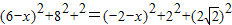 ,得
,得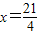 ,
,
经检验,此时点N在线段BC上,
所以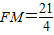 .
.
方法二:
(Ⅰ)解:取线段EF的中点H,AF的中点G,连接A′G,A′H,GH.
因为A′E=A′F及H是EF的中点,
所以A′H⊥EF
又因为平面A′EF⊥平面BEF,
所以A′H⊥平面BEF,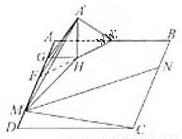
又AF?平面BEF,
故A′H⊥AF,
又因为G、H是AF、EF的中点,
易知GH∥AB,
所以GH⊥AF,
于是AF⊥面A′GH,
所以∠A′GH为二面角A′-DH-C的平面角,
在Rt△A′GH中,A′H=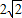 ,GH=2,A'G=
,GH=2,A'G=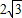
所以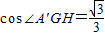 .
.
故二面角A′-DF-C的余弦值为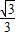 .
.
(Ⅱ)解:设FM=x,
因为翻折后,C与A′重合,
所以CM=A′M,
而CM2=DC2+DM2=82+(6-x)2,
A′M2=A′H2+MH2=A′H2+MG2+GH2=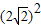 +(2+x)2+22,
+(2+x)2+22,
故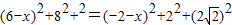
得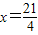 ,
,
经检验,此时点N在线段BC上,
所以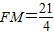 .
.
点评:空间两条直线夹角的余弦值等于他们方向向量夹角余弦值的绝对值;
空间直线与平面夹角的余弦值等于直线的方向向量与平面的法向量夹角的正弦值;
空间锐二面角的余弦值等于他的两个半平面方向向量夹角余弦值的绝对值;
(1)取线段EF的中点H,连接A′H,因为A′E=A′F及H是EF的中点,所以A′H⊥EF,又因为平面A′EF⊥平面BEF.则我们可以以A的原点,以AE,AF,及平面ABCD的法向量为坐标轴,建立空间直角坐标系A-xyz,则锐二面角A′-FD-C的余弦值等于平面A′FD的法向量,与平面BEF的一个法向量夹角余弦值的绝对值.
(2)设FM=x,则M(4+x,0,0),因为翻折后,C与A重合,所以CM=A′M,根据空间两点之间距离公式,构造关于x的方程,解方程即可得到FM的长.
解答:解:(Ⅰ)取线段EF的中点H,连接A′H,因为A′E=A′F及H是EF的中点,所以A′H⊥EF,
又因为平面A′EF⊥平面BEF.
如图建立空间直角坐标系A-xyz
则A′(2,2,
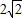 ),C(10,8,0),
),C(10,8,0),F(4,0,0),D(10,0,0).
故
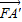 =(-2,2,2
=(-2,2,2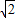 ),
),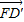 =(6,0,0).
=(6,0,0).设
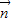 =(x,y,z)为平面A′FD的一个法向量,
=(x,y,z)为平面A′FD的一个法向量,-2x+2y+2
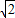 z=0
z=0所以6x=0.

取
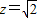 ,则
,则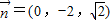 .
.又平面BEF的一个法向量
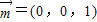 ,
,故
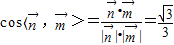 .
.所以二面角的余弦值为
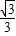
(Ⅱ)设FM=x,则M(4+x,0,0),
因为翻折后,C与A重合,所以CM=A′M,
故,
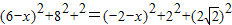 ,得
,得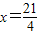 ,
,经检验,此时点N在线段BC上,
所以
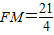 .
.方法二:
(Ⅰ)解:取线段EF的中点H,AF的中点G,连接A′G,A′H,GH.
因为A′E=A′F及H是EF的中点,
所以A′H⊥EF
又因为平面A′EF⊥平面BEF,
所以A′H⊥平面BEF,

又AF?平面BEF,
故A′H⊥AF,
又因为G、H是AF、EF的中点,
易知GH∥AB,
所以GH⊥AF,
于是AF⊥面A′GH,
所以∠A′GH为二面角A′-DH-C的平面角,
在Rt△A′GH中,A′H=
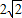 ,GH=2,A'G=
,GH=2,A'G=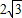
所以
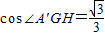 .
.故二面角A′-DF-C的余弦值为
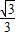 .
.(Ⅱ)解:设FM=x,
因为翻折后,C与A′重合,
所以CM=A′M,
而CM2=DC2+DM2=82+(6-x)2,
A′M2=A′H2+MH2=A′H2+MG2+GH2=
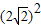 +(2+x)2+22,
+(2+x)2+22,故
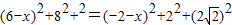
得
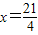 ,
,经检验,此时点N在线段BC上,
所以
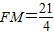 .
.点评:空间两条直线夹角的余弦值等于他们方向向量夹角余弦值的绝对值;
空间直线与平面夹角的余弦值等于直线的方向向量与平面的法向量夹角的正弦值;
空间锐二面角的余弦值等于他的两个半平面方向向量夹角余弦值的绝对值;

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
 如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD.
如图,在矩形ABCD中,AB=2BC,P,Q分别为线段AB,CD的中点,EP⊥平面ABCD. 如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点.
如图,在矩形ABCD中,已知AB=2AD=4,E为AB的中点,现将△AED沿DE折起,使点A到点P处,满足PB=PC,设M、H分别为PC、DE的中点. 如图,在矩形ABCD中,AB=3
如图,在矩形ABCD中,AB=3 如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系:
如图,在矩形ABCD中,已知AB=3,AD=1,E、F分别是AB的两个三等分点,AC,DF相交于点G,建立适当的平面直角坐标系: 如图,在矩形ABCD中,AB=
如图,在矩形ABCD中,AB=