题目内容
已知函数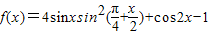 .
.(1)设ω>0为常数,若
 上是增函数,求ω的取值范围;
上是增函数,求ω的取值范围;(2)设集合
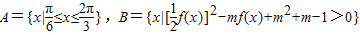 ,若A?B恒成立,求实数m的取值范围.
,若A?B恒成立,求实数m的取值范围.
【答案】分析:(1)利用三角函数的降幂公式将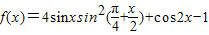 化为f(x)=2sinx,从而f(ωx)=2sinωx,利用f(ωx)在[
化为f(x)=2sinx,从而f(ωx)=2sinωx,利用f(ωx)在[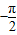 ,
,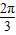 ]是增函数,可得到
]是增函数,可得到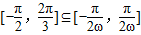
,从而可求ω的取值范围;
(2)由于f(x)=2sinx,将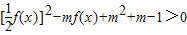 化为sin2x-2msinx+m2+m-1>0,令sinx=t,则t2-2mt+m2+m-1>0,t∈[
化为sin2x-2msinx+m2+m-1>0,令sinx=t,则t2-2mt+m2+m-1>0,t∈[ ,1],记f(t)=t2-2mt+m2+m-1,
,1],记f(t)=t2-2mt+m2+m-1,
问题转化为上式在t∈[ ,1]上恒成立问题,根据区间[
,1]上恒成立问题,根据区间[ ,1]在对称轴t=m的左侧,右侧,对称轴穿过区间[
,1]在对称轴t=m的左侧,右侧,对称轴穿过区间[ ,1]三种情况结合二次函数的单调性即可解决.
,1]三种情况结合二次函数的单调性即可解决.
解答:(本小题满分14分)
解:(1)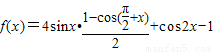 =2sinx(1+sinx)-2sin2x=2sinx.
=2sinx(1+sinx)-2sin2x=2sinx.
∵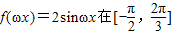 是增函数,
是增函数,
∴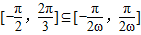
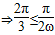 ,∴
,∴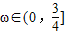
(2)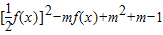
=sin2x-2msinx+m2+m-1>0
因为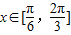 ,设sinx=t,则t∈[
,设sinx=t,则t∈[ ,1]
,1]
上式化为t2-2mt+m2+m-1>0
由题意,上式在t∈[ ,1]上恒成立.
,1]上恒成立.
记f(t)=t2-2mt+m2+m-1,
这是一条开口向上抛物线,
则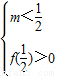
或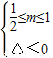
或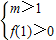
解得: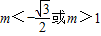 .
.
点评:本题考查二倍角的余弦,二次函数的性质,难点在于转化与构造函数,利用f(t)=t2-2mt+m2+m-1>0恒成立,t∈[ ,1]来解决,属于难题.
,1]来解决,属于难题.
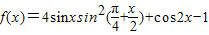 化为f(x)=2sinx,从而f(ωx)=2sinωx,利用f(ωx)在[
化为f(x)=2sinx,从而f(ωx)=2sinωx,利用f(ωx)在[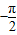 ,
,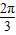 ]是增函数,可得到
]是增函数,可得到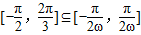
,从而可求ω的取值范围;
(2)由于f(x)=2sinx,将
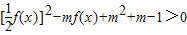 化为sin2x-2msinx+m2+m-1>0,令sinx=t,则t2-2mt+m2+m-1>0,t∈[
化为sin2x-2msinx+m2+m-1>0,令sinx=t,则t2-2mt+m2+m-1>0,t∈[ ,1],记f(t)=t2-2mt+m2+m-1,
,1],记f(t)=t2-2mt+m2+m-1,问题转化为上式在t∈[
 ,1]上恒成立问题,根据区间[
,1]上恒成立问题,根据区间[ ,1]在对称轴t=m的左侧,右侧,对称轴穿过区间[
,1]在对称轴t=m的左侧,右侧,对称轴穿过区间[ ,1]三种情况结合二次函数的单调性即可解决.
,1]三种情况结合二次函数的单调性即可解决.解答:(本小题满分14分)
解:(1)
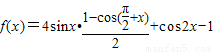 =2sinx(1+sinx)-2sin2x=2sinx.
=2sinx(1+sinx)-2sin2x=2sinx.∵
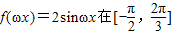 是增函数,
是增函数,∴
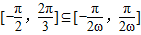
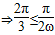 ,∴
,∴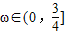
(2)
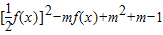
=sin2x-2msinx+m2+m-1>0
因为
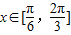 ,设sinx=t,则t∈[
,设sinx=t,则t∈[ ,1]
,1]上式化为t2-2mt+m2+m-1>0
由题意,上式在t∈[
 ,1]上恒成立.
,1]上恒成立.记f(t)=t2-2mt+m2+m-1,
这是一条开口向上抛物线,
则
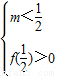
或
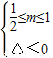
或
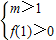
解得:
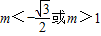 .
.点评:本题考查二倍角的余弦,二次函数的性质,难点在于转化与构造函数,利用f(t)=t2-2mt+m2+m-1>0恒成立,t∈[
 ,1]来解决,属于难题.
,1]来解决,属于难题. 
练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
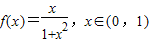 .
. ;
; 的最小值.
的最小值. .
. 的值域.
的值域.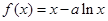 ,
,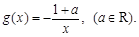
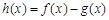 ,求函数
,求函数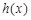 的单调区间;
的单调区间;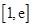 (
(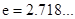 )上存在一点
)上存在一点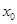 ,使得
,使得
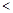
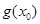 成立,求
成立,求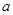 的取值范围.
的取值范围.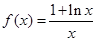 .
.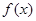 在区间
在区间 上存在极值,求实数a的取值范围;
上存在极值,求实数a的取值范围;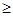 1时,不等式
1时,不等式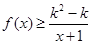 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围. 与
与
 分别相交于点
分别相交于点 ,且曲线
,且曲线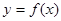 和
和 在点
在点 的值;
的值; 为
为 的导函数,若对于任意的
的导函数,若对于任意的 ,
, 恒成立,求实数
恒成立,求实数 的最大值;
的最大值; 倍时,当
倍时,当 时,若函数
时,若函数 的最小值恰为
的最小值恰为 的最小值,求实数
的最小值,求实数 的值
的值