题目内容
已知函数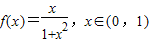
．（1）设x1，x2∈（0，1），证明：（x1-x2）•[f（x1）-f（x2）]≥0；
（2）设x∈（0，1），证明：
；（3）设x1，x2，x3都是正数，且x1+x2+x3=1，求
的最小值．
【答案】分析：（1）将函数代入并进行化简即可得证；
（2）利用（1）的结论得
，经化简即可证明；
（3）利用（2）的结论，代入化简
可得最小值
解答：解：（1）
，故得证；
（2）由（1）得
，即
整理得
，从而得证；
（3）由（2）得
，即最小值为0
点评：本题的考点是函数与方程的综合运用，主要考查已知函数解析式，证明不等式即求函数则最值，注意上下小题之间的联系．
（2）利用（1）的结论得
，经化简即可证明；（3）利用（2）的结论，代入化简
可得最小值解答：解：（1）
，故得证；（2）由（1）得
，即整理得，从而得证；（3）由（2）得
，即最小值为0点评：本题的考点是函数与方程的综合运用，主要考查已知函数解析式，证明不等式即求函数则最值，注意上下小题之间的联系．
练习册系列答案
相关题目
．
，求f（x）的值域．
．
的值域．
．
的值域．
．
（ω＞0）在区间
上是增函数的ω的最大值．