题目内容
如图,在三棱柱![]() 中,
中,
![]() 是正方形
是正方形![]() 的中心,
的中心,![]() ,
,![]() 平面
平面![]() ,且
,且![]()
(Ⅰ)求异面直线AC与A1B1所成角的余弦值;
(Ⅱ)求二面角![]() 的正弦值;
的正弦值;
(Ⅲ)设![]() 为棱
为棱![]() 的中点,点
的中点,点![]() 在平面
在平面![]() 内,且
内,且![]() 平面
平面![]() ,求线段
,求线段![]() 的
的
长.
|
.本小题主要考查异面直线所成的角、直线与平面垂直、二面角等基础知识,考查用空间向量解决立体几何问题的方法,考查空间想象能力、运算能力和推理论证能力.满分13分.
方法一:如图所示,建立空间直角坐标系,点B为坐标原点.
依题意得![]()
![]()
 |
(I)解:易得![]() ,
,
于是
所以异面直线AC与A1B1所成角的余弦值为![]()
(II)解:易知![]()
设平面AA1C1的法向量![]() ,
,
则 即
即
不妨令![]() 可得
可得![]() ,
,
同样地,设平面A1B1C1的法向量![]() ,
,
则 即
即 不妨令
不妨令![]() ,
,
可得![]()
于是![]()
从而![]()
所以二面角A—A1C1—B的正弦值为![]()
(III)解:由N为棱B1C1的中点,
得![]() 设M(a,b,0),
设M(a,b,0),
则![]()
由![]() 平面A1B1C1,得
平面A1B1C1,得
即
解得 故
故![]()
因此![]() ,所以线段BM的长为
,所以线段BM的长为![]()
方法二:
(I)解:由于AC//A1C1,故![]() 是异面直线AC与A1B1所成的角.
是异面直线AC与A1B1所成的角.
因为![]() 平面AA1B1B,又H为正方形AA1B1B的中心,
平面AA1B1B,又H为正方形AA1B1B的中心,
![]()
可得![]()
因此![]()
所以异面直线AC与A1B1所成角的余弦值为![]()
 |
(II)解:连接AC1,易知AC1=B1C1,
又由于AA1=B1A1,A1C1=A1=C1,
所以![]() ≌
≌![]() ,过点A作
,过点A作![]() 于点R,
于点R,
连接B1R,于是![]() ,故
,故![]() 为二面角A—A1C1—B1的平面角.
为二面角A—A1C1—B1的平面角.
在![]() 中,
中,![]()
连接AB1,在![]() 中,
中,
![]()
![]() ,
,
从而![]()
所以二面角A—A1C1—B1的正弦值为![]()
(III)解:因为![]() 平面A1B1C1,所以
平面A1B1C1,所以![]()
取HB1中点D,连接ND,由于N是棱B1C1中点,
所以ND//C1H且![]() .
.
又![]() 平面AA1B1B,
平面AA1B1B,
所以![]() 平面AA1B1B,故
平面AA1B1B,故![]()
又![]()
所以![]() 平面MND,连接MD并延长交A1B1于点E,
平面MND,连接MD并延长交A1B1于点E,
则![]()
由![]()
得![]() ,延长EM交AB于点F,
,延长EM交AB于点F,
可得![]() 连接NE.
连接NE.
在![]() 中,
中,
![]()
所以![]()
可得![]()
连接BM,在![]() 中,
中,
![]()

 阅读快车系列答案
阅读快车系列答案
 如图,在三棱柱中,已知AB⊥侧面BB1C1C,
如图,在三棱柱中,已知AB⊥侧面BB1C1C,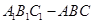 中,
中,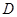 ,
,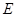 ,
,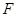 分别为
分别为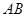 ,
, ,
,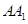 的中点,设三棱锥
的中点,设三棱锥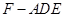 体积为
体积为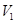 ,三棱柱
,三棱柱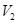 ,则
,则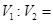

 中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则
中,侧棱垂直于底面,底面是边长为2的正三角形,侧棱长为3,则 与平面
与平面 所成的角是
所成的角是
 B.
B. C.
C.  D.
D.
 中,
中, 侧面
侧面 ,且
,且 与底面成
与底面成 角,
角, ,则该棱柱体积的 最小值为
.
,则该棱柱体积的 最小值为
. 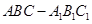 中,
中,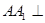 面
面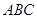 ,
,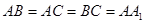 ,
,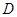 ,
,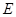 分别为
分别为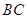 ,
,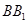 的中点.
的中点.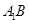 ∥平面
∥平面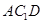 ; (2)求证:
; (2)求证: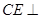 平面
平面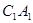 与平面
与平面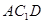 所成的角的正弦值.
所成的角的正弦值.