题目内容
如图,在正四棱柱ABCD—A1B1C1D1中,AA1=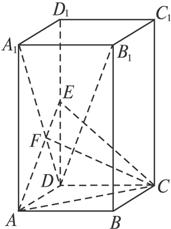
(1)求直线B1D和平面A1ADD1所成角的大小;
(2)求证:B1D⊥AE;
(3)求二面角C-AE-D的大小.
解法一:(1)解:连结A1D.
∵ABCD—A1B1C1D1是正四棱柱,

∴A1B1⊥平面A1ADD1.
∴A1D是B1D在平面A1ADD1上的射影.
∴∠A1DB1是直线B1D和平面A1ADD1所成的角.
在Rt△B1A1D中,tan∠A1DB1=![]() =
=![]() ,
,
∴∠A1DB1=30°.
即直线B1D和平面A1ADD1所成角的大小是30°.
(2)证明:在Rt△A1AD和Rt△ADE中,
∵![]() =
=![]() =
=![]() ,∴△A1AD∽△ADE.
,∴△A1AD∽△ADE.
∴∠A1DA=∠AED.
∴∠A1DA+∠EAD=∠AED+∠EAD=90°.
∴A1D⊥AE.
由(1)知,A1D是B1D在平面A1ADD1上的射影,
根据三垂线定理,得B1D⊥AE.
(3)解:设A1D ∩AE=F,连结CF.
∵CD⊥平面A1ADD1,且AE⊥DF,
根据三垂线定理,得AE⊥CF,
∴∠DFC是二面角CAED的平面角.
在Rt△ADE中,由AD·DE=AE·DF![]() DF=
DF=![]() =
=![]() .
.
在Rt△FDC中,tan∠DFC=![]() =
=![]() ,
,
∴∠DFC=60°,
即二面角CAED的大小是60°.
解法二:∵ABCD—A1B1C1D1是正四棱柱,
∴DA、DC、DD1两两互相垂直.
如图,以D为原点,直线DA,DC,DD1分别为x轴,y轴,z轴,建立空间直角坐标系.
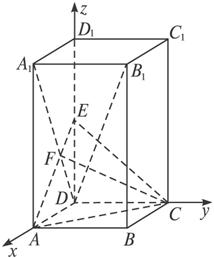
则D(0,0,0),A(1,0,0),B(1,1,0),C(0,1,0),B1(1,1,2)
(1)解:连结A1D,∵ABCD—A1B1C1D1是正四棱柱,
∴A1B1⊥平面A1ADD1.
∴A1D是B1D在平面A1ADD1上的射影.
∴∠A1DB1是直线B1D和平面A1ADD1所成的角.
∵A1(1,0,![]() ),∴
),∴![]() =(1,0,
=(1,0,![]() ),
),![]() =(1,1,
=(1,1,![]() ),
),
∴cos〈![]() ,
,![]() 〉=
〉=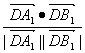 =
=![]() .
.
∴∠A1DB1=30°,
即直线B1D和平面A1ADD1所成角的大小是30°.
(2)证明:∵E是DD1的中点,
∴E(0,0,![]() ).∴
).∴![]() =(-1,0,
=(-1,0,![]() ).
).
∵![]() =-1+0+1=0,
=-1+0+1=0,
∴B1D⊥AE.
(3)解:设A1D∩AE=F,连结CF.
∵CD⊥平面A1ADD1,且AE⊥DF,
根据三垂线定理,得AE⊥CF,
∴∠DFC是二面角C-AE-D的平面角.
根据平面几何知识,可求得F(![]() ,0,
,0,![]() ),
),
∴![]() =(
=(![]() ,0,-
,0,-![]() ),
),![]() =(
=(![]() ,1,-
,1,-![]() ).
).
∴cos〈![]() ,
,![]() 〉=
〉=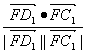 =
=![]() ,
,
∴二面角C-AE-D的大小是60°.

 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=
如图,在正四棱柱ABCD-A′B′C′D′中(底面是正方形的直棱柱),侧棱AA′=| 3 |
| 2 |
| A、30° | B、45° |
| C、60° | D、90° |
 如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=4,AB=2,E是棱CC1上的一个动点.
如图,在正四棱柱ABCD-A1B1C1D1中,已知AA1=4,AB=2,E是棱CC1上的一个动点. (2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a,
(2012•青岛一模)如图,在正四棱柱ABCD-A1B1C1D1中,AB=a, 如图,在正四棱柱ABCD-A1B1C1D1中,AA1=A(x0,y0)AB=2,点E、M分别为A1B、C1C的中点.
如图,在正四棱柱ABCD-A1B1C1D1中,AA1=A(x0,y0)AB=2,点E、M分别为A1B、C1C的中点. (2009•宜昌模拟)如图,在正四棱柱ABCD-A1B1C1D1 中,AB=BC=1,AA1=2.过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于60°,这样的直线l最多可作( )
(2009•宜昌模拟)如图,在正四棱柱ABCD-A1B1C1D1 中,AB=BC=1,AA1=2.过顶点D1在空间作直线l,使l与直线AC和BC1所成的角都等于60°,这样的直线l最多可作( )