圆C过点P(1,2)和Q,且圆C在两坐标轴上截得的弦长相等,求圆C的方程. 题目和参考答案——青夏教育精英家教网—

题目内容

圆C过点P(1,2)和Q(-2,3),且圆C在两坐标轴上截得的弦长相等,求圆C的方程.

x²+y²+2x-2y-3=0或x²+y²+4x+4y-17=0.

解析:

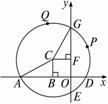
如图所示,由于圆C在两坐标轴上的弦长相等,即|AD|=EG|,所以它们的一半也相等,即|AB|=|GF|.

又|AC|=|GC|,

∴Rt△ABC≌Rt△GFC.

∴|BC|=|FC|.

设C(a,b),则|a|=|b|.①

又圆C过点P(1,2)和Q(-2,3),

∴圆心在PQ的垂直平分线上,

即,即y=3x+4.∴b=3a+4.②

由①知a=±b,代入②

∴或5.

故所求的圆的方程为(x+1)²+(y-1)²=5或(x+2)²+(y+2)²=25,

即x²+y²+2x-2y-3=0或x²+y²+4x+4y-17=0.

练习册系列答案

中考英语话题复习浙江工商大学出版社系列答案

，2）作圆C的切线，求切线的方程；
（Ⅲ）过点P作两条相异直线分别与圆C相交A，B两点，设直线PA和直线PB的斜率分别为k，-k，O为坐标原点，试判断直线OP和直线AB是否平行？请说明理由．

已知点O为坐标原点，圆C过点（1，1）和点（-2，4），且圆心在y轴上．
（1）求圆C的标准方程；
（2）如果过点P（1，0）的直线l与圆C有公共点，求直线l的斜率k的取值范围；
（3）如果过点P（1，0）的直线l与圆C交于A、B两点，且|AB|=2

，试求直线l的方程．

已知圆C过点P(1，1)，且与圆(x＋3)²＋(y＋3)²＝r²(r＞0)关于直线x＋y＋3＝0对称．

(1)求圆C的方程；

(2)过点P作两条直线分别与圆C相交于点A、B，且直线PA和直线PB的倾斜角互补，O为坐标原点，判断直线OP与AB是否平行，并请说明理由．

（本小题满分16分）
已知圆C过点P(1，1)，且与圆M：＋＝(r＞0)关于直线x＋y＋2＝0对称．
（1）求圆C的方程；
（2）直线l过点Q(1，0.5),截圆C所得的弦长为2,求直线l的方程；
（3）过点P作两条相异直线分别与圆C相交于A，B，且直线PA和直线PB的倾斜角互补，O为坐标原点，试判断直线OP和AB是否平行？请说明理由．

试题分类