题目内容
(本小题满分l2分)(注意:在试题卷上作答无效)
已知O为坐标原点,F为椭圆![]() 在y轴正半轴上的焦点,过F且斜率为
在y轴正半轴上的焦点,过F且斜率为![]() 的直线
的直线![]() 与C交与A、B两点,点P满足
与C交与A、B两点,点P满足![]()
(Ⅰ)证明:点P在C上;
(II)设点P关于O的对称点为Q,证明:A、P、B、Q四点在同一圆上。
解:(I)F(0,1),![]() 的方程为
的方程为![]() ,
,
代入![]() 并化简得
并化简得
![]() …………2分
…………2分
设![]()
则![]()
![]()
由题意得![]()
所以点P的坐标为![]()
经验证,点P的坐标为![]() 满足方程
满足方程
![]() 故点P在椭圆C上。 …………6分
故点P在椭圆C上。 …………6分
(II)由![]() 和题设知,
和题设知, ![]()
PQ的垂直一部分线![]() 的方程为
的方程为
![]() ①
①
设AB的中点为M,则![]() ,AB的垂直平分线为
,AB的垂直平分线为![]() 的方程为
的方程为
![]() ②
②
由①、②得![]() 的交点为
的交点为![]() 。 …………9分
。 …………9分
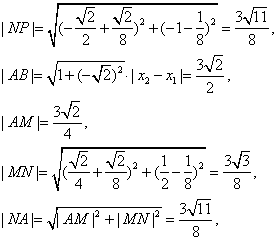
故|NP|=|NA|。
又|NP|=|NQ|,|NA|=|NB|,
所以|NA|=|NP|=|NB|=|MQ|,
由此知A、P、B、Q四点在以N为圆心,NA为半径的圆上 …………12分

练习册系列答案
相关题目
 ,bn+1=-
,bn+1=- Sn(n∈N*).
Sn(n∈N*). +
+ +…+
+…+ ,求Tn的表达式
,求Tn的表达式 ,过左焦点
,过左焦点 作直线
作直线 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线 交于点
交于点 .
. 为直径的圆经过焦点
为直径的圆经过焦点 .
. :函数
:函数 (
( )的值域是
)的值域是 ;命题
;命题 :指数函数
:指数函数 在
在 上是减函数.若命题“
上是减函数.若命题“ 的范围.
的范围. 并且与曲线
并且与曲线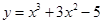 相切的直线方程.
相切的直线方程.