题目内容
已知命题p:夹角为m的单位向量a,b使|a-b|>l,命题q:函数f(x)=msin(mx)的导函数为f′(x),若?xo∈R, .设符合p∧q为真的实数m的取值的集合为A.
.设符合p∧q为真的实数m的取值的集合为A.
(I)求集合A;
(Ⅱ)若B={x∈R|x2=πa},且B∩A=∅,求实数a的取值范围.
解:(I)∵| -
- |>1,|
|>1,| |=|
|=| |=1
|=1
∴ 2+
2+ 2-2
2-2 •
• =2-2cosm>1
=2-2cosm>1
∴cosm<
∵0≤m≤π
∴ <m≤π
<m≤π
即命题p为真时,m的取值对应的集合P=( ,π]
,π]
函数f(x)=msin(mx)的导函数f′(x)=m2cos(mx),
若?xo∈R, .则f′(x)max=m2≥
.则f′(x)max=m2≥
解得m≤- 或m≥
或m≥ ,
,
p∧q为真,即p和q都为真,此时有 <m≤π且m≤-
<m≤π且m≤- 或m≥
或m≥ ,
,
即 ≤m≤π
≤m≤π
故实数m的取值的集合为A=[ ,π].
,π].
(II)(1)若B=∅,满足B∩A=∅,
此时实数a的取值范围a<0;
(2)若B≠∅,则a≥0,此时B={x|x=± },
},
由B∩A=∅,得 ,或
,或 ,
,
∴0≤a≤ ,或a
,或a .
.
综上,实数a的取值范围是(-∞, ]∪[
]∪[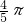 ,+∞).
,+∞).
分析:(I)分别求出命题为真时,参数的范围,再根据p∧q为真,则p真q真,建立不等式组,从而可求实数m的取值范围.
(II)由条件A∩B=φ,对字母a分类讨论,我们易构造出一个关于a的不等式,解此不等式即可得到实数a的取值范围.
点评:本题的考点是集合的包含关系判断及应用,主要考查集合的关系、集合的运算,同时考查向量运算与导数的应用.集合关系中的参数取值问题,其中根据已知条件,构造出关于a的不等式组,是解答本题的关键.本题是一个中档题目.
 -
- |>1,|
|>1,| |=|
|=| |=1
|=1∴
 2+
2+ 2-2
2-2 •
• =2-2cosm>1
=2-2cosm>1∴cosm<

∵0≤m≤π
∴
 <m≤π
<m≤π即命题p为真时,m的取值对应的集合P=(
 ,π]
,π]函数f(x)=msin(mx)的导函数f′(x)=m2cos(mx),
若?xo∈R,
 .则f′(x)max=m2≥
.则f′(x)max=m2≥
解得m≤-
 或m≥
或m≥ ,
,p∧q为真,即p和q都为真,此时有
 <m≤π且m≤-
<m≤π且m≤- 或m≥
或m≥ ,
,即
 ≤m≤π
≤m≤π故实数m的取值的集合为A=[
 ,π].
,π].(II)(1)若B=∅,满足B∩A=∅,
此时实数a的取值范围a<0;
(2)若B≠∅,则a≥0,此时B={x|x=±
 },
},由B∩A=∅,得
 ,或
,或 ,
,∴0≤a≤
 ,或a
,或a .
.综上,实数a的取值范围是(-∞,
 ]∪[
]∪[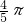 ,+∞).
,+∞).分析:(I)分别求出命题为真时,参数的范围,再根据p∧q为真,则p真q真,建立不等式组,从而可求实数m的取值范围.
(II)由条件A∩B=φ,对字母a分类讨论,我们易构造出一个关于a的不等式,解此不等式即可得到实数a的取值范围.
点评:本题的考点是集合的包含关系判断及应用,主要考查集合的关系、集合的运算,同时考查向量运算与导数的应用.集合关系中的参数取值问题,其中根据已知条件,构造出关于a的不等式组,是解答本题的关键.本题是一个中档题目.

练习册系列答案
相关题目
 .设符合p∧q为真的实数m的取值的集合为A.
.设符合p∧q为真的实数m的取值的集合为A. .设符合p∧q为真的实数m的取值的集合为A.
.设符合p∧q为真的实数m的取值的集合为A.