题目内容
已知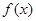 为定义在
为定义在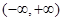 上的可导函数,且
上的可导函数,且 对于
对于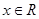 恒成立,且
恒成立,且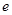 为自然对数的底,则( )
为自然对数的底,则( )
A.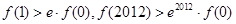 |
B.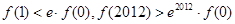 |
C.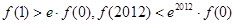 |
D.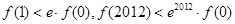 |
A
解析试题分析:因为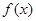 为定义在
为定义在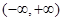 上的可导函数,且
上的可导函数,且 ,则说明
,则说明 单调递增,同时当x>0时,则
单调递增,同时当x>0时,则
故选A.
考点:函数的单调性与其导函数关系
点评:本题主要考查函数的单调性与其导函数的关系,函数单调性的关系,考查转化、构造、计算能力

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
已知函数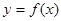 的导函数
的导函数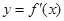 的图像如下,则( )
的图像如下,则( )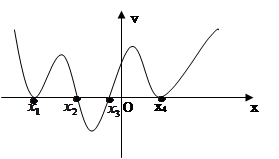
A.函数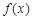 有1个极大值点,1个极小值点 有1个极大值点,1个极小值点 |
B.函数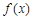 有2个极大值点,2个极小值点 有2个极大值点,2个极小值点 |
C.函数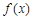 有3个极大值点,1个极小值点 有3个极大值点,1个极小值点 |
D.函数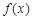 有1个极大值点,3个极小值点 有1个极大值点,3个极小值点 |
下列函数中,周期为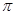 ,且在区间
,且在区间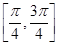 上单调递增的函数是
上单调递增的函数是
A.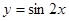 | B.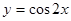 | C.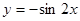 | D.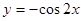 |
如果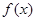 为偶函数,且
为偶函数,且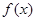 导数存在,则
导数存在,则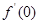 的值为 ( )
的值为 ( )
| A.2 | B.1 | C.0 | D.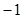 |
当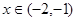 时,不等式
时,不等式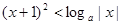 恒成立,则实数
恒成立,则实数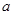 取值范围是( )
取值范围是( )
| A.[2,+∞) | B.(1,2] | C.(1,2) | D.(0,1) |
函数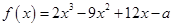 恰有两个不同的零点,则
恰有两个不同的零点,则 可以是( )
可以是( )
| A.3 | B.4 | C.6 | D.7 |
定义在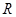 上的可导函数
上的可导函数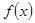 ,已知
,已知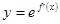 的图像如图所示,则
的图像如图所示,则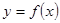 的增区间是( )
的增区间是( )
A.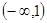 | B. | C.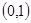 | D.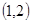 |
下列两个函数相等的是( )
A.y=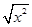 与y=x 与y=x | B.y=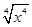 与y=|x| 与y=|x| |
C.y=|x|与y=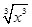 | D.y=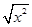 与y= 与y=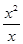 |
下列函数为奇函数,且在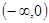 上单调递减的函数是( )
上单调递减的函数是( )
A.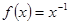 | B.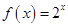 | C.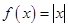 | D.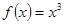 |